Do you remember what you ate and drank during the first thousand days of your life? Probably not. Either way, everything you consumed back then played a vital role in your development. Not only did it help your bones grow and your brain develop, it also shaped a community of bacteria, fungi, and viruses, collectively known as microbes, that lives inside your gut. This community is called the gut microbiome, which is responsible for digesting your food and protecting you against diseases. But how does it do that?
The gut microbiome works hard to keep you healthy, and it expects to be rewarded with a generous supply of nutrients in return. Thus, it will be happier if you drink a smoothie rich in nutrients like vitamins, minerals, and antioxidants, instead of a sugary soda. In the case of a sugary soda, your microbes wouldn’t receive enough nutrients, making it harder for them to do their job effectively. This makes it difficult for you to maintain a healthy weight and avoid illness, especially at an early age. Simply put, treating your gut badly increases the risk of overweight.
Typically, it is more difficult for households with a tight budget to give the gut what it desires; a sugary soda is a more practical choice than a rich smoothie. Essentially, there exists a relationship between socioeconomic status and overweight. The health of the gut microbiome plays an important role in this relationship. That's why in 2023 the METAHEALTH project was launched to tackle this issue.
I had the opportunity to work on this project for my bachelor’s thesis. My thesis was part of the theme In silico modelling, which aims at developing and validating mathematical models to numerically simulate the interplay between microbiome, lifestyle, culture and environment, as well as their effects on oral and metabolic health during the first 1000 days of life. Huub Hoefsloot, who is a researcher at the Swammerdam Institute for Life Sciences at the University of Amsterdam and co-supervised my thesis, is one of the people working in this theme in METAHEALTH.
In our research we want to understand how various substances, like carbs, sugars or fibres, affect the human microbiome in the first 1000 days of life. Mathematical models can be very useful in this process, as we can freely experiment with various interventions. How does an increase in carbs affect the interactions between bacteria in your gut for example? They offer much more flexibility than experiments in the lab. Designing experiments in the lab can be very difficult because of all the parameters you must consider so that it can resemble what happens in our bodies. Recent biological models like "gut on a chip" can be combined with the insights we get from mathematical models based on the Navier-Stokes equations so that we can develop efficient interventions to improve the health of the gut microbiome. - Huub Hoefsloot
I focused on simulating the flow through the gut, or gut flow for short. To accomplish this, we will use the Navier-Stokes equations like Huub mentioned.
From microbiome to model
You might be wondering, “How is gut flow connected to the gut microbiome?” Think of gut flow like a conveyor belt transporting nutrients through the gut for hungry microbes to grab. This is difficult to observe by looking at the microbiome directly; there are trillions of microbes inside your gut—more than the number of stars in our galaxy—so you can’t keep track of them all. I developed a mathematical model that mimics this conveyor belt which controls the amount of nutrients you can place onto it. Not only could this reveal how the microbiome reacts to different nutrient levels inside a real gut, but also how the microbiome is distributed throughout the gut in order to grab these nutrients.
To understand how we can model gut flow, let’s consider a simple example. Imagine you’re drinking a healthy smoothie—as recommended by your gut microbiome—through a plastic straw. In this scenario, the straw represents your gut, and the smoothie flows toward your mouth as you suck it in, simulating gut flow. As long as you don’t suck too hard, the smoothie will flow in the same direction through the entire straw, but there are small differences in the speed of this flow. The smoothie flows relatively slowly near the plastic, increasing in speed the closer you get to the center of the straw. This speed, together with its direction, is what we refer to as velocity.
The math behind the movement
It may seem complicated to describe the differences in velocity of a fluid like a smoothie mathematically, but you actually only need two equations! In 1822, the French engineer Claude-Louis Navier published his work on fluid flow, which was refined by the Irish mathematician George Stokes two decades later, resulting in the aptly named Navier-Stokes equations.
Both equations require you to be familiar with some mathematical notation. To start, we need to make a map of the gut. We don't look at an anatomical map that you may see in a biology textbook, but a map that describes the velocity of fluid in every point within the gut. For this purpose, we use a vector denoted as . Some amount of fluid enters and some amount of fluid leaves every point, but this amount doesn’t have to be the same. This relates to what we call divergence. A positive divergence means more fluid leaves the point than enters it. A negative divergence means the opposite. If you want to have balanced gut flow, the divergence must be neither positive nor negative. So, the divergence () needs to be zero everywhere. This gives us the first of the Navier-Stokes equations, which is the continuity equation: \begin{equation} \text{div } \mathbf{V} = 0. \end{equation} The above guarantees a balanced gut flow, but it does not describe motion. To understand the second of the Navier-Stokes equations—the momentum equation—let's recall Newton's second law of motion that you may have seen in a physics course. It states that the mass of an object (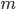) multiplied by its acceleration (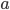) equals the force that acts upon the object (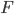): \begin{equation} ma = F. \end{equation}
The momentum equation is very similar. In the case of fluid, we don't speak of mass, but of density (). Furthermore, you may recall that acceleration is the derivative of velocity. A mathematical way or writing this derivative is . This gives us a new left-hand side of the equation above. On the right side, we had the total force that acts on the object. We now speak of the forces acting on the fluid in a single point, of which there are three:
The first force comes from the pressure differences within the fluid (), similar to air pushing against a balloon from the inside.
The second is gravity () pulling the fluid downwards depending on the density (). The denser ("heavier") a fluid, the more gravity will pull it down.
The third arises from friction within the fluid, which depends on its viscosity (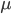), a measure of the fluid's thickness. A higher viscosity means more friction, which is why it's harder to stir honey than water. It also depends on the second derivative of the velocity () in that point. Why exactly this is the case is outside the scope of this article.
We end up with the following equation: \begin{equation} \rho \frac{D\mathbf{V}}{Dt} = -\nabla p + \rho \mathbf{g} + \mu \nabla^2 \mathbf{V}. \end{equation}
Making it more realistic
The Navier-Stokes equations describe fluid flow in general. To apply them specifically to gut flow, we have to add some features of the gut. First, the gut wall affects the flow in two ways. The muscles in the wall push the contents of the gut, much like the conveyor belt moving nutrients, and the wall absorbs water along with some nutrients, allowing our body to benefit from these nutrients. Both of these features can be added to the model using what’s called a boundary condition, which dictates how the walls behave in our mathematical version of the gut. The second change involves the viscosity inside the gut, which varies throughout, yet it’s assumed to be a fixed value in the momentum equation. This might seem inconsequential, but it leads to very different solutions!
Speaking of solutions: how do we obtain them? We can’t solve the Navier-Stokes equations exactly because of how complex fluid flow is. This means we cannot find a formula for how the fluid moves through the gut over time. Instead, we describe mathematically where there is fluid in the gut. Then, we approximate how this fluid will flow using an algorithm. The algorithm begins by estimating the velocities in all points and then repeatedly refining these values based on the previous estimate. It repeats this process until the estimates barely change anymore, meaning the refinement no longer has a notable effect. Research on gut flow has also been conducted inreal guts inside living humans. I compared my results with these results from scientific literature. As it turns out, this algorithm produces solutions that match the flow inside a real gut!
My experience with METAHEALTH
It was satisfying to end up with a working model after months of effort, but what I gained from this journey was even more valuable. This was my first real experience as an applied mathematician, a title that might suggest my only task was to find the correct mathematical tools and apply them. However, I quickly realized that it’s practically impossible to use the Navier-Stokes equations—which I hadn’t even heard of before my bachelor’s thesis!—without understanding what they mean and how to derive them. Having the right tool isn’t enough; you need to get comfortable with the tool before you can start using it productively.
The most valuable to me was that I could make a (small) contribution to an important cause like METAHEALTH by developing a model which simulates gut flow. This model may help to understand the relationship between nutrient intake and the gut microbiome. In the future, METAHEALTH plans to expand this model by taking more factors into account, such as the interactions between microbes. Ultimately, the knowledge obtained from the model can unlock some of the gut microbiome’s secrets, making it possible to develop new treatments for overweight children in the future. Until then, let’s show our microbiomes some appreciation by drinking some smoothies—but not too many, or you will consume too much sugar!
Two weeks ago I had the pleasure to attend two events where prizes for outstanding research in mathematics were awarded, one of them was the CWI Best Thesis in Applied Math 2024. It was a great pleasure to be there, to chat with (most of) the candidates, and to learn what they have done during their bachelor and master thesis'.
We want our guts to be filled with a diverse range of mutually beneficial and competitive interactions, a perfect blend of friends, frenemies, and enemies to keep our guts active and body on its toes. Read how networks can help understand these interactions!
After having a near-fatal accident falling off his horse, Prussian footman Hans Berger (1873—1941) was surprised to learn that his sister had—being kilometers away—him a telegram to let him know that she sensed he was in grave danger.
How can one hope to understand the precise structure of a virus if it is able to become unrecognizable within weeks? The mathematics behind this questions didn't let go of my mind for extensive periods of time during my PhD studies in Belgium.
. Some amount of fluid enters and some amount of fluid leaves every point, but this amount doesn’t have to be the same. This relates to what we call divergence. A positive divergence means more fluid leaves the point than enters it. A negative divergence means the opposite. If you want to have balanced gut flow, the divergence must be neither positive nor negative. So, the divergence (
) needs to be zero everywhere. This gives us the first of the Navier-Stokes equations, which is the continuity equation: \begin{equation} \text{div } \mathbf{V} = 0. \end{equation} The above guarantees a balanced gut flow, but it does not describe motion. To understand the second of the Navier-Stokes equations—the momentum equation—let's recall Newton's second law of motion that you may have seen in a physics course. It states that the mass of an object (
) multiplied by its acceleration (
) equals the force that acts upon the object (
): \begin{equation} ma = F. \end{equation}
). Furthermore, you may recall that acceleration is the derivative of velocity. A mathematical way or writing this derivative is 
. This gives us a new left-hand side of the equation above. On the right side, we had the total force that acts on the object. We now speak of the forces acting on the fluid in a single point, of which there are three:
), similar to air pushing against a balloon from the inside.
) pulling the fluid downwards depending on the density (
), a measure of the fluid's thickness. A higher viscosity means more friction, which is why it's harder to stir honey than water. It also depends on the second derivative of the velocity (
) in that point. Why exactly this is the case is outside the scope of this article.
