We have now seen two very simple properties that the number of friends that people in friendship networks should satisfy. Recall that the number of connections of a network element is called its degree. In this part, we take this a little further by introducing and investigating the degree sequence of a network, or graphs as the abstract mathematical term is.
The degree sequence of a graph is the sequence of degrees of all its elements. Thus, when the graph has 100 elements, the degree sequence consists of 100 numbers that tell us what the degree is of each of the network elements. For a friendship network, this corresponds to the number of friends that each individual has. Part I explained that the sum of these numbers must be even as it is twice the number of connections in the network, and that each of these numbers is at most the number of network elements minus one. But are all sequences that satisfy these properties possible?
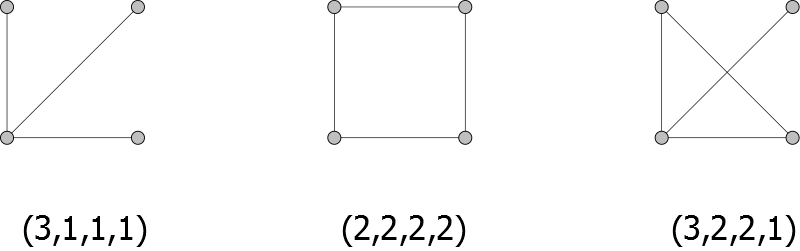
Let us investigate this further with examples of small graphs. For a network of 3 vertices, there are essentially 4 different possible conntion patterns, depending on the total number of connections, which can be 0,1,2 or 3. See the figure below. Of course, we may as well assume that the degrees go from large to small, meaning that the first vertex has the highest degree, the second vertex has the second largest degree, etc. We can swap them around if this is not the case, and it certainly reduces the number of possibilities!
We see that the degree sequences for the four possible graphs of three elements are given by
(0,0,0) (1,1,0) (2,1,1) (2,2,2)
respectively. As it turns out, these are also precisely all possible sequences where the largest value is at most 2 (the number of vertices minus one), and their sum is even. So, while this may give insight, this does not yet answer the question which degree sequences are possible! Bear in mind that we are assuming that our networks are simple, meaning that the elements cannot be connected to themselves and pairs of elements have only one edge between them.
We continue with graphs of four elements. We may as well assume that all degrees are at least 1, since if there is an element that does not have any edges, then the degree sequence is just one of the above 4 sequences with an extra 0 at the end corresponding to the element without any connections. So, we will assume that each number in the degree sequence is at least 1. This means that there can be two to six edges in total. All possible graphs of four elements are then the following six:
Any other collection of degrees is impossible. For example, the sequence (3,3,1,1), which does not appear in the above list, is impossible. Indeed, the two degrees three correspond to two elements that must be connected to all other network elements. But then the other two elements need to have at least 2 connections, and thus cannot have degree 1. We conclude that certainly not all sequences can be proper degree sequences, even when their sum is even and their largest is at most the number of elements minus one. Note, by the way, that it is crucial here that we are dealing with simple networks, where elements cannot be connected to themselves and pairs of elements can have at most one connection between them. Indeed, the degree sequence (3,3,1,1) can be realized if we either allow for self-loops or for multiple edges. Find these graphs yourself!
We call sequences that can arise as degree sequences of simple graphs graphical. This immediately raises the question which sequences are graphical and which are not. There is a beautiful criterion by Erdős and Gallai that resolves this question, and even suggests an explicit network corresponding to a graphic degree sequence. This is what we explain in the next piece of this serial.
Have you ever found yourself less popular when compared to your friends? Interestingly, in any group of individuals, on average, people have fewer friends than their friends do, or at the very most, an equal number. Not more!
In this article, we will discuss a mathematical riddle that "seems impossible even if you know the answer". It is better known as the 100 prisoners problem.
