Or what a graph theoretist would say: Any regular bipartite graph has a perfect matching
It is a Saturday. Sam and his friends like to get together and play cards during the weekend. This Saturday they planned to come to Sam's house in the afternoon to play cards. Sam just finished lunch and started waiting his friends. ‘Maybe I need to find something to pass the time’, Sam yawned. There was a deck of cards near him, which was for the afternoon card game.
Excluding two jokers, there are thirteen ranks in the pack: A (Ace), 2,..., 10, J (Jack), Q (Queen) and K (King), with four cards in each rank (clovers, diamonds, hearts, and spades). Cards are always like magic for Sam. They are simple, but there is a variety of ways to play. In his spare time, Sam likes to play with the cards to see if he can get something new. He picked up the deck and removed the two Jokers. In the card game he plays with his friends, Jokers are often used as informal replacements for lost or damaged cards. He shuffled the deck. Sam always wants things to be even and perfect, so he divided the cards into thirteen piles of four cards each:
Pile 1: 8 10 6 9 Pile 2: 9 2 A 4 Pile 3: 3 8 Q K Pile 4: 9 2 10 J Pile 5: 7 5 J Q Pile 6: 4 Q 2 2 Pile 7: Q 8 6 7 Pile 8: K 10 8 K Pile 9: 7 K 7 J Pile 10: 5 J 4 A Pile 11: 9 6 A A Pile 12: 5 6 10 4 Pile 13: 3 5 3 3
Sam looked at the 13 piles. Suddenly, a question came to his mind. ‘Can I pick one card from each of the 13 piles so that there is exactly one card with each rank?’ He asked himself.
Take some time to experiment yourself and see if you can answer this question.
Sam tried it by hand, first picking a 3 from the last pile. Since there were 3 3s in this pile, he believed that if there was a solution for his question, 3 would most likely be chosen from the last deck. Then he picked a 2 from pile 6, a K from pile 8 and an Ace from pile 11... Sam found he succeeded easily:
Sam shuffled the deck many more times and he always managed to find the desired 13 cards!
Feel free to play around and check this by yourself, sometimes you may get stuck, but try to see how you could circumvent the dead ends.
Matching Cards
Time passed quickly and the doorbell rang. It was Sam’s friend, Jackie. They went to high school together and were quite close. Sam and Jackie spent a lot of time playing cards together at that time. Jackie is also very interested in puzzles about cards. After high school, Sam went to study medicine, while Jackie studied math at the same university, so they still played cards together sometimes. Now Jackie is a mathematician. Sam greeted Jackie and then shared the problem with her. It would be so perfect if he could always pick up such 13 cards. After hearing Sam’s problem, Jackie smiled knowing that what would follow would surprise and impress Sam.
Jackie: Just as perfect as you wish, you can always find a way to do that.
Sam: That’s so great! But how can you answer me so quickly? Is there any math behind this question?
Jackie: Yes, there is a mathematical result stating that every regular bipartite graph has a perfect matching. This result implies that you can always choose such 13 cards! I know this may not be the perfect time for this, but it is a very cool mathematical argument and I really want to discuss it with you, although it may take some time and patience form your side!
Jackie was wondering if she wanted to start explaining this result, since mathematicians are often quite shy and hesitant to start a discussion about mathematics. Which should not be the case, since mathematics is a world full of interesting and creative results!
But it may take some time and patience to understand them, so bear with us and Sam in this quest to understand why you can select all 13 ranks from 13 piles of cards. Always!
Jackie: Sam, the first step is to translate our card problem to a question on so-called graphs. To keep the explanation simpler, I will explain you why this result is true using only the cards A, 2, 3, 4, 5, 6. In this case, we have 6 different ranks and we make 6 piles of 4 cards each. You can then think of the case of all 13 ranks and 13 piles on your own. Using the piles of cards, we construct a graph. We do this as follows.
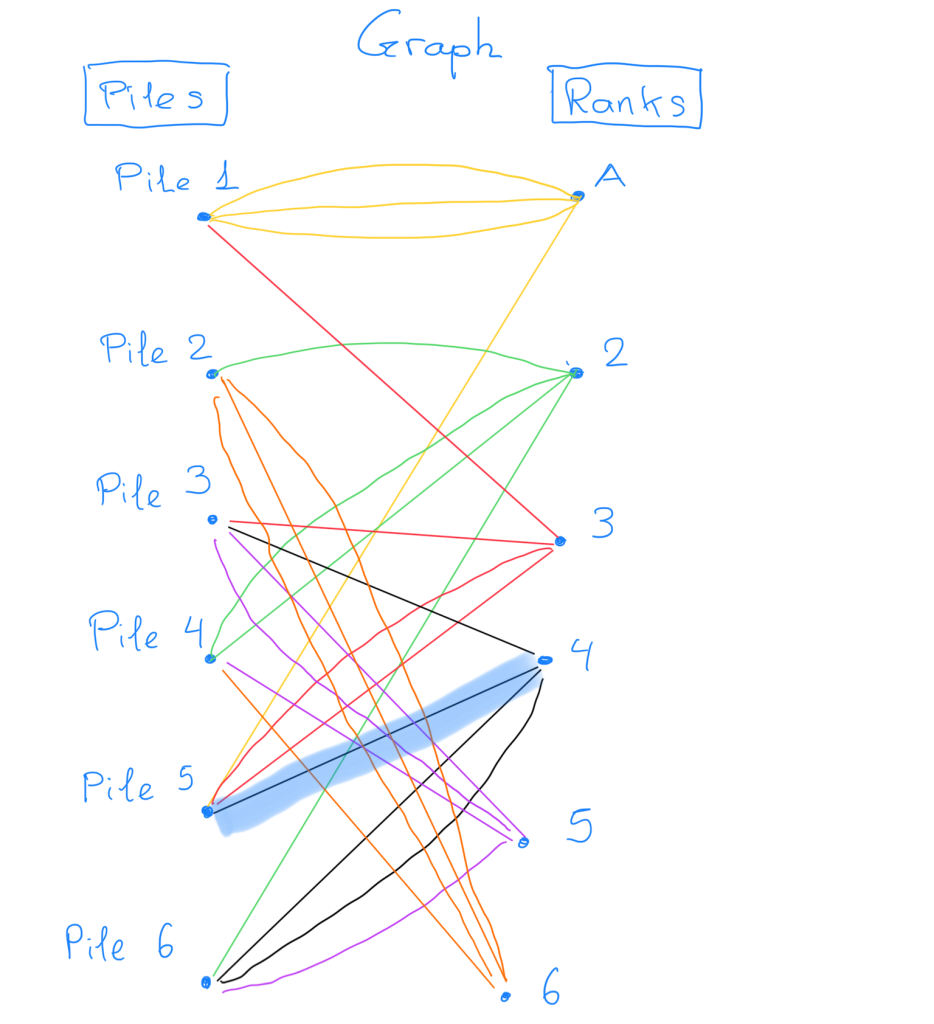
We make two groups of points, six vertices on the left which represent the piles, and six vertices on the right which represent the ranks. If a pile has a card of a certain rank, an edge is drawn between this pile and the rank. This edge represents the corresponding card in the pile; if there are several cards of the same rank in the pile, same amount of edges are drawn between the pile and the rank. Consider, for example, the following piles.
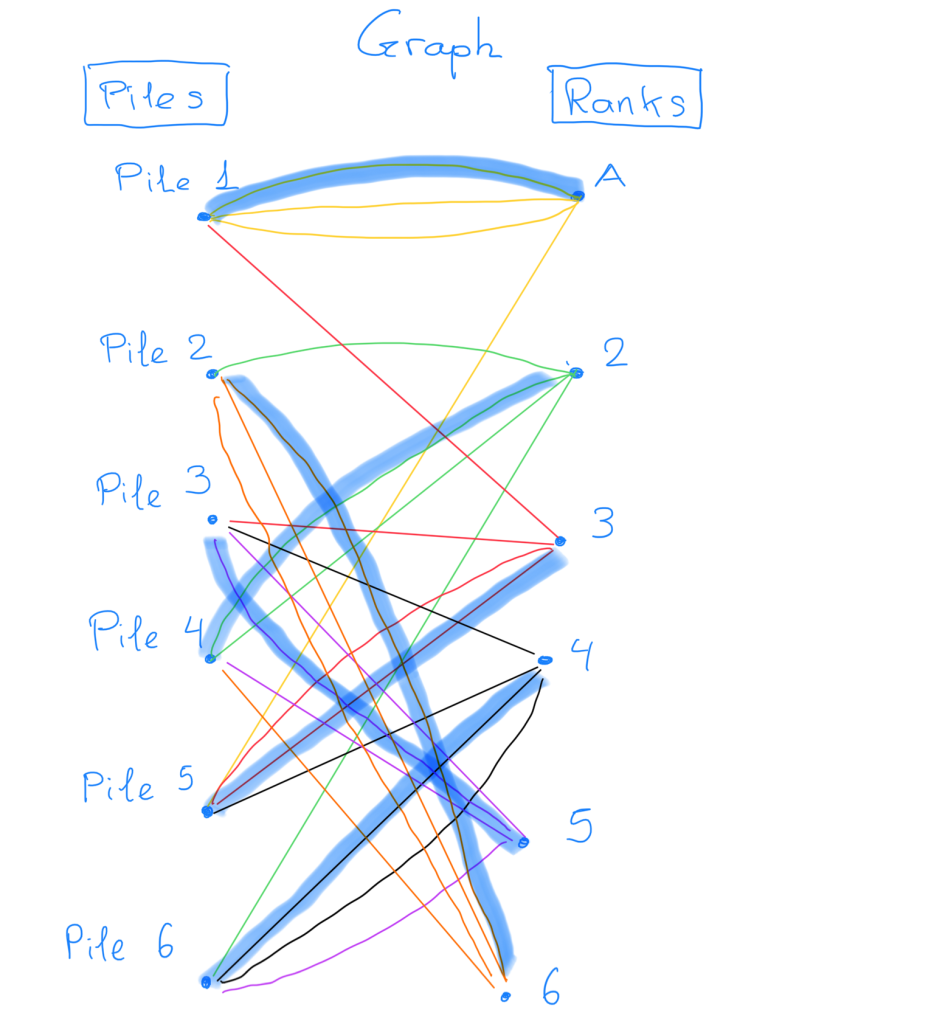
Pile 1: A A 3 A Pile 2: 6 6 6 2 Pile 3: 5 5 4 3 Pile 4: 2 5 2 6 Pile 5: 4 3 3 A Pile 6: 2 4 4 5
In the shuffle above we get the following graph
A graph which contains two groups of vertices, and each vertex is only connected to the vertices in the other group, is called a bipartite graph.
Jackie: This is the first ingredient of the mathematical result. Sam, as a small test that you get this, do you want to draw the bipartite graph corresponding to the following piles?
Pile 1: 2 3 4 5, Pile 2: A A 2 2 Pile 3: 6 6 4 3, Pile 4: 5 5 5 2, Pile 5: 6 A 3 4, Pile 6: 4 6 A 3
Perfection is in the eye of the mathematician
This bipartite graph is regular, meaning that every vertex is connected to the same number of other vertices. Each vertex is part of four edges, which makes sense since each pile contains four cards, and there are four cards in each rank. But why is this translation of the problem to a graph useful?
We claim that there is a way to draw one card from each pile and get all 6 ranks. Drawing a rank from a pile is the same as picking an edge from the graph! Picking 3 from Pile 1 is the same as picking the red edge between vertex “Pile 1” and vertex “Rank 3”. Hence picking ranks from piles is equivalent to picking edges in the graph.
Jackie: Sam, do you see how the problem of choosing 1 rank from each pile translates to choosing edges from this graph?
Sam: Hm, I am not sure I follow Jackie.
Jackie: We said that picking an edge in the graph corresponds to picking a card (the vertex on the right of the edge) from a certain pile (the vertex on the left of the edge). Right?
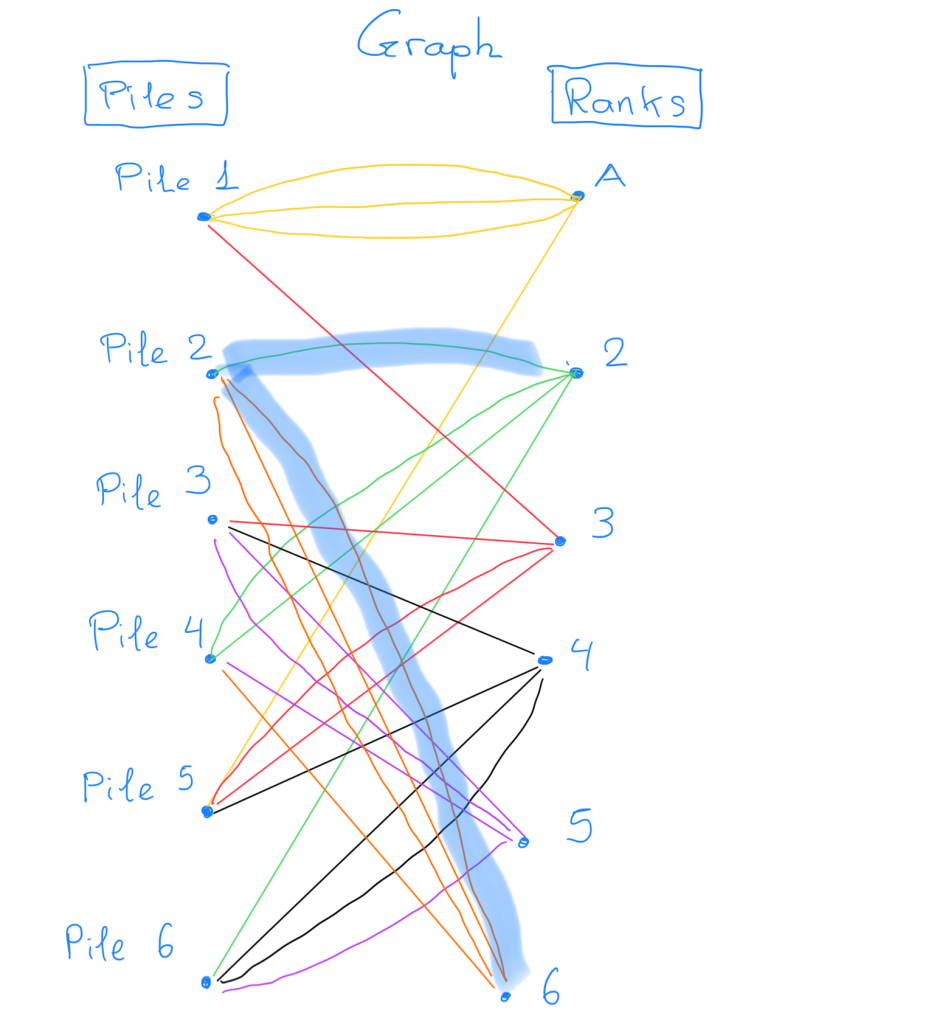
Picking a card from a pile is the same as picking an edge from the graph. For example, picking a 4 from Pile 5 is the same as picking the black edges connections vertices “Pile 5” and “Rank 4”.
Sam: Yes. So, we want to choose 6 edges from the graph.
Jackie: Exactly! But which edges?
Sam: Such that all 6 ranks appear, and we draw 1 card from each pile?
Jackie: Perfect! So, you want to pick 6 edges which have no vertices in common with each other.
Sam: Because if you pick two edges which share a vertex, then either you will be drawing two cards from the same pile, or you will be picking two times the same rank.
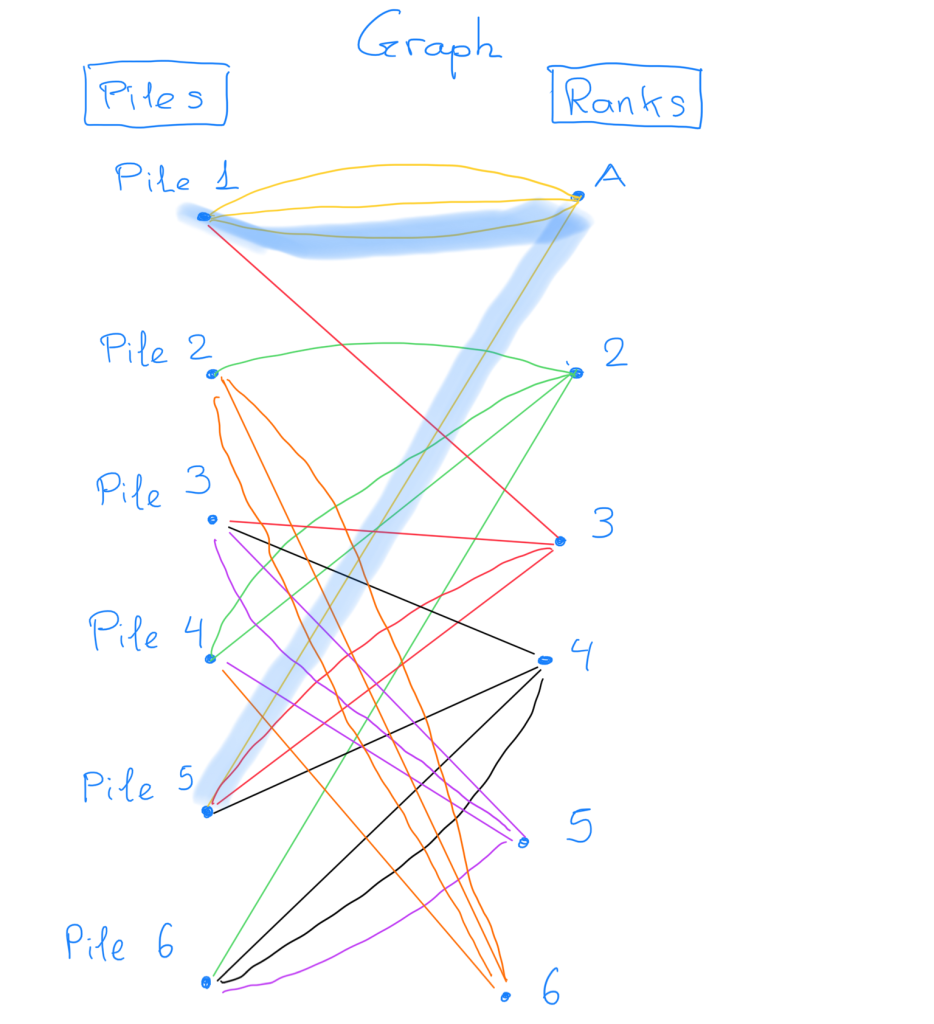
Pick two edges sharing a vertex is not allowed. If they share a vertex “left” then we pick two cards from the same pile, if they share a vertex “right” then we pick the same rank twice.
Jackie: Wonderful! You really get it!
Hence, we want to make a ‘perfect matching’ in this bipartite graph. This means we choose 6 edges that share no common vertices, neither on the left side, nor on the right side! This is exactly what that mathematical result states! In every regular bipartite graph there is always a perfect matching!
Look at the blue edges in our bipartite graph, they form a perfect matching. All vertices are in some edges, and no vertex is part of more than one edge!
Sam: That’s so interesting! Can you tell me why that statement is true?
Jackie: I would love to! But let's do that tomorrow with a cup of tea, and now we can focus on the game!
Not long after, Sam's other poker friends arrived. This time, as usual, it was Jackie who won the most. While playing cards, Sam was still engrossed in his question. He is amazed by the beauty of cards, and the beauty of math.
In Part 1 Jackie explained to her fried Sam how the problem of picking a card from each of the 13 piles so that there is exactly one card with each rank translates to a problem on bipartite graphs. The mathematical problem asks you to find a perfect matching in a regular bipartite graph.
Are you one of those people who always seems to pack just a bit too much for your car to handle when packing for a vacation? Then you should have a look at this article!
Have you ever wondered what kind of insights you can gain about games by looking at it using a mathematical lens? In this article we have a look at Snakes and Ladders, and in a follow up article we will dive into Monopoly!
