Alexander Grothendieck (1928—2014) is viewed by many as one of the greatest mathematicians of all time. He made contributions to many different fields, but the work he is mainly celebrated for is his shaping of some of the most abstract, fundamental branches of mathematics, such as category theory and algebraic geometry. (Besides being a great mathematician he also led a fascinating life, well worth reading about.)
One important contribution that Grothendieck made was the idea of “stacks”, which is the name of a certain idea that plays an important role in algebraic geometry. Stacks are abstract, complicated objects. So complicated, in fact, that even most mathematicians don’t know how they work. To know this to some usable degree requires several years of study.
And if that weren’t bad enough, there is basically no good book to explain it. Grothendieck himself was famous for not being very good at explaining stuff (much of his later work took the form of long handwritten diaries that also contained autobiographical essays, and weren’t intended for publication). But even in the sixty years since his discovery of stacks, other, more businesslike mathematicians have struggled to bring the concept into the light.
In 2005, a number of algebraic geometrists finally had enough of the rather ridiculous situation that one of their central ideas, stacks, was so far out of reach as to be (almost) unusable. To remedy the situation they started an ambitious new project, simply called “the stacks project”.
The goal of the stacks project was straightforward: create a website that explains stacks.
Now, twelve years later, the stacks project is an immense, incredibly useful resource for anyone who wants to learn about stacks, or modern algebraic geometry in general. By nature, it is still highly specialized, but for someone who knows enough about mathematics, it makes the subject much more accessible.
Now it should be said that algebraic geometry has almost nothing to do with the mathematics of networks. For networks, we study very specific objects, often with very clear applications in mind. Algebraic geometry, on the other hand, tries to find some of the most fundamental truths about the shapes of mathematical functions. (For example, about the locations of the roots of a polynomial, for all possible polynomials at once).
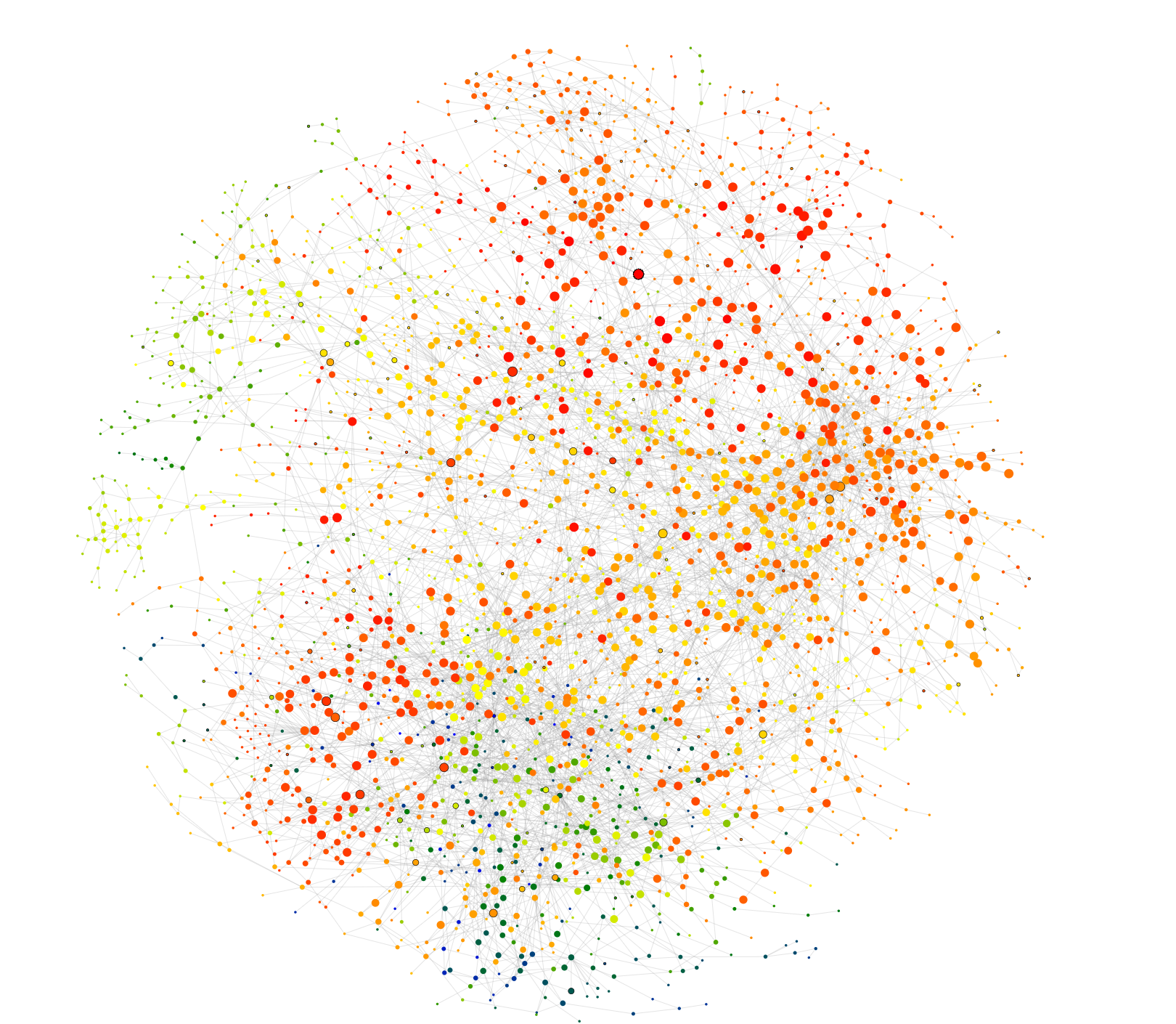
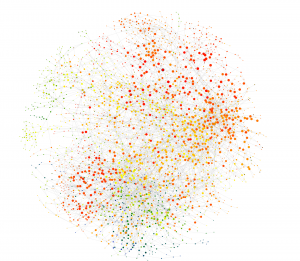
But even though we can't really use it, the stacks project provides us with an amazing example of a network: namely, a network of mathematical ideas. The website allows you to visualize beautifully how a certain mathematical idea is related to other ideas, by showing you where the idea is used, and which other ideas it uses. Mapping this for every separate idea, a network naturally arises.
The website offers different settings to view the network. And it is possible to visualize the depth of the network (how many steps of logic two different ideas are removed). The chains of reasoning are remarkably long (no small-world phenomenon here, it seems.) It would be very interesting to analyze this network mathematically, for instance, by looking at typical distances and the degree sequences. As far as I know, this hasn’t been done yet.
Two weeks ago I had the pleasure to attend two events where prizes for outstanding research in mathematics were awarded, one of them was the CWI Best Thesis in Applied Math 2024. It was a great pleasure to be there, to chat with (most of) the candidates, and to learn what they have done during their bachelor and master thesis'.
Two weeks ago I had the pleasure to attend two events where prizes for outstanding research in mathematics were awarded, the Christiaan Huygens Science prize and the CWI Best Thesis in Applied Math 2024.
On the 5th of July, the Fields medals 2022 were awarded to four mathematicians. The four mathematicians that won the Fields medals this year are: Hugo Duminil-Copin, June Huh, James Maynard. and Maryna Viazovska.
In this article, dear reader, I am going to show you in which way the development of your opinion during the last political issue, the spread of a virus among your acquaintances during the current pandemic, and the alignment of some particles lying inside the device from which you are reading this article are extremely comparable phenomena.
