On 11 May 2020 Prof. dr. Aida Beatrijs Paalman-de Miranda passed away. Aida (Ietje) Paalman-de Miranda was professor of mathematics between 1966 and 1997 at the Korteweg-de Vries Institute, the mathematics research institute of the University of Amsterdam.
Aida B. Paalman-de Miranda was born in Surinam in 1936 and traveled at the age of 17 to The Netherlands, where she studied mathematics at the University of Amsterdam. In a recent article in the NRC we read about Paalman-de Miranda:
“she was a mathematician that loved her field, pure mathematics, and specifically topology and set theory.”
Paalman-de Miranda did her doctorate under the supervision of the famous topologist Prof. Johannes de Groot at the Mathematisch Centrum (today CWI). In 1966 she became a lecturer and some years later a full-professor in pure mathematics. She was moreover the first woman professor in mathematics at the University of Amsterdam.
To commemorate Paalman-de Miranda I would like to describe in this short article the area of mathematics that she loved and devoted her career to, topology.
Topology
Topology is the field of mathematics that studies deformations of geometric objects. Not all kind of deformations are allowed though, topologists are interested in the so called continuous deformations, such as stretching, twisting, bending. Tearing is one of the deformations that is not allowed for example. To fully understand what continuous deformations are, think of a sphere made of rubber or play dough. By stretching and bending it you can turn the sphere into various other geometric objects, these are all called continuous transformations of the sphere. On the contrary making a hole into it is not a continuous transformation.
In topology such continuous transformations are called homeomorphisms. For topologists, two geometric objects that can be transformed into each other using only such homeomorphisms are considered to be equivalent. Mathematically stated, such objects are called topologically equivalent.
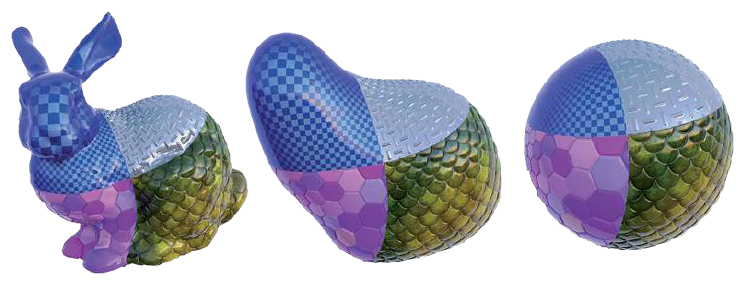
These three geometrical objects are topologically equivalent. The rather complicated shape of the rabbit is simplified by transforming it to that of the sphere. This picture is taken from the article Het vormen van ruimte: van Poincaré tot Perelman by Ronald van der Veen, Nieuw Archief voor Wiskunde, Maart 2014.
An other funny example is that of a cup and the donut, formally called the torus, which can also be transformed into each other using continuous transformations. This fact gave birth to the joke that a topologist can’t see the difference between a donut and a coffee mug.
On the other hand, a torus and a sphere are not topologically equivalent since the torus has a hole which we can’t make by applying only continuous transformations on the sphere. You must be wondering now how all these ideas came to exist and why were people intrigued people to think of deformations of geometrical objects. Amazingly enough, the answer to this questions came from space and the movement of the planets!
The French mathematician Henri Poincaré.
The French mathematician Henri Poincaré is considered to be the father of topology. At the end of the 19th century many scientists were studying the movement of the planets and were trying to understand various properties of this rather complex mechanical system called the solar system. In his research Poincaré made a remarkable observation, that the exact form of the equations used to study the movement of the planets was sometimes not so important. And that if you changed the equations a little bit, many aspects of the solutions remained unchanged.
When studying global properties of a system, like the movement of the planets in the solar system, it is sufficient to look at the global properties of the solutions of the equations of movement and you can disregard some details.
Poincaré needed thus a methodology, and the corresponding mathematical language, to study global properties of mechanical systems. This was nicely phrased by Ronald van der Veen in an article for the Dutch mathematics magazine Nieuw Archief voor Wiskunde in his question
“What remains from geometry if we disregard irrelevant details like angles, distances and straight lines?”
In order to approach this question Poincaré started developing a beautiful mathematical theory called topology. Therefore, in topology it doesn’t matter if you work with a ball or with a rabbit-shaped object, since both of these objects are topologically equivalent. The big advantage though is that the ball is much easier to work with. But you cannot use the ball if you want to study the torus, since these two objects are not equivalent. Hence an important question in topology, a question that bothered the great Poincaré and keeps bothering mathematicians until today, concerns the classification of geometrical objects in groups of topologically equivalent objects. How many of such basic topological objects are there besides the ball and the torus?
Around 1900 Poincaré himself tried to give an answer to this question by studying quite simple objects. His work and his ideas regarding this issue gave birth to the notorious Poincaré conjecture, an extremely difficult mathematical problem as history has shown. Explaining this conjecture in detail is far from the scope of this article but it is rather scary and impressive to say that, although the conjecture was posed in 1900, a complete answer was given in 2003 by the Russian mathematician Grigori Perelman! The conjecture remained unsolved for about 100 years!
One ingredient of the answer to Poincaré’s conjecture is Euler's formula, have a look at my previous blog to learn more about this. If you would like to have a deeper look into Poincaré's conjecture and it’s solution and to see why Euler's formula is important I refer to this wonderful article (in Dutch) written by Ronald van der Veen.
To conclude I would like to go back to Paalman-de Miranda’s work. As mentioned before she was a topologist. More specifically, her research concerned a concept in topology called topological groups. The objects discussed above, the sphere, the torus etc, yield in topology what we call topological spaces. A topological group is an extension of a topological space. It is a topological space where we can also add and multiply elements, the term group in the name refers to this additional feature. The theory of topological groups started being developed around 1850, pioneers of this theory were various great mathematicians like Sophus Lee and Felix Klein. Topological groups are very important in modern research, not only in topology, but in mathematics in general and in physics as well.
On the occasion of Paalman-De Miranda’s death I spent my day reading about topology, this wonderful mathematical theory which has inspired many scientists and has received a lot of attention during the last century. Moreover, the Netherlands has a profound legacy in topology and Paalman-De Miranda’s work added a significant contribution to this legacy. As a small conceptual exercise I would say, have a look at the space around you and at all the objects in it and classify them into classes of topologically equivalent objects! Have fun doing a little bit of topology.
From February 26th until March 1st, we had the unique opportunity to visit the Anton de Kom University in Suriname. The goal of our visit was to assess possibilities for cooperation between our mathematics institute and the math department in Paramaribo.
During the last decades, many resources have been invested in quantum computing. This research field has grown immensely and amazing results have been obtained. The plans for the future are highly ambitious, but at the same time, there are serious questions that need to be addressed.
In this article Maya continues her journey from Rotterdam to Brussels. She starts thinking about a puzzle from her childhood, the three utilities problem. At the end of the jouney she has reached a very important theorem from graph theory!
