How Math Solved the Billiard Table

In this video, we explain periodic trajectories and explore how many exist on a billiard table. We will take you on a small journey where we will look at this problem from an unexpected perspective. We hope you enjoy it!
Interview with Claudia Flandoli, author of comics and an illustrator

Claudia Flandoli is an author of comics and an illustrator, with a keen interest in science topics. Last year she gave a short talk during the opening of IMAGINARY in Amsterdam. We couldn't let this opportunity pass and we asked her for an interview about art and science.
Could the Future of Artificial Intelligence be Self-Organising?

One of the main building blocks of modern AI-tools are artificial neural networks, abstract models inspired by the structure and functions of biological neural networks which enable machines to "learn". In this article, I will discuss some thoughts on this topic.
Tales of the Tails: (Not so) mysterious Heavy Tail worldbeyond the Bell Curve

The scientific world would not be what it is today without normal distribution. It is the foundation of many statistical models for several good reasons. Most importantly, it appears commonly in nature. But this is only the tip of the iceberg.
What is neighborhood centrality and what is it good for?

In the study of social networks, a key phenomena is the diffusion of information – how it travels from one individual to another across the network of people. An important question is how to identify the nodes with a high potential to spread information widely and deeper in the network.
Microbiome: the mysterious stock exchange in your gut

We want our guts to be filled with a diverse range of mutually beneficial and competitive interactions, a perfect blend of friends, frenemies, and enemies to keep our guts active and body on its toes. Read how networks can help understand these interactions!
Some ideas on teaching graph theory in high schools
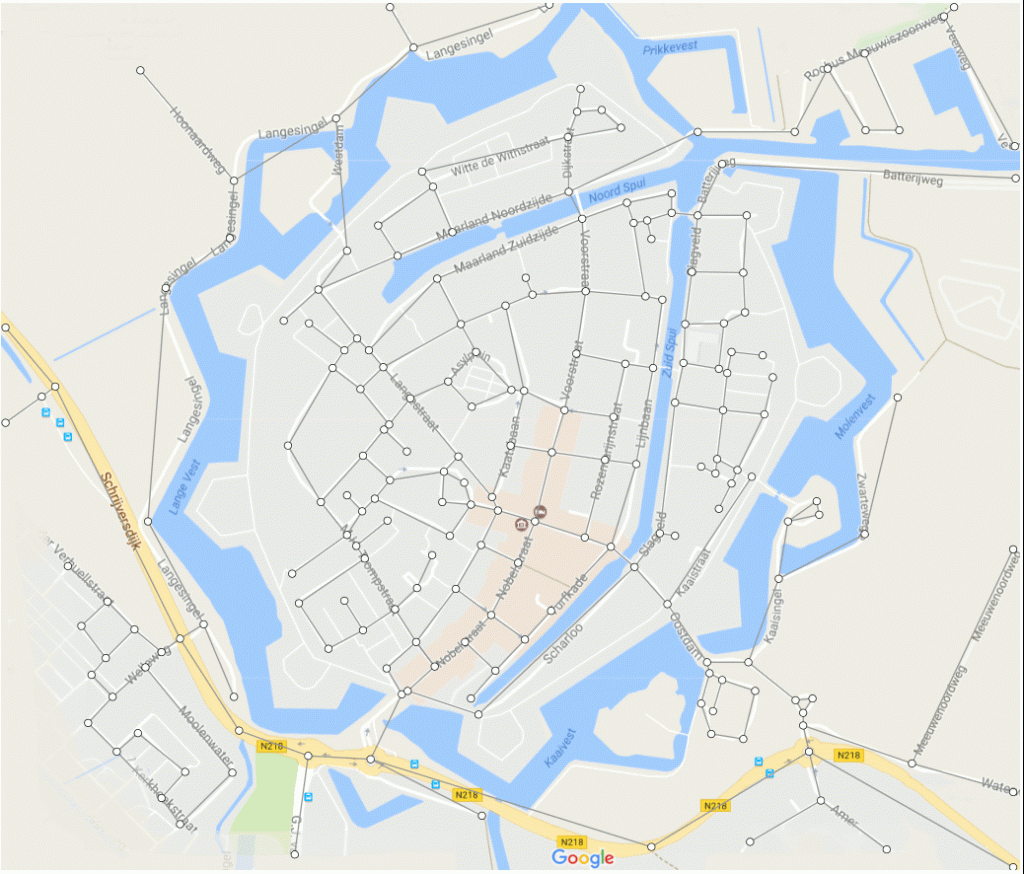
Have you ever wondered how you can make mathematics interesting to the daily life of students? In this article, we will discuss two important and exciting concepts teachers can use to introduce graph theory in their classes.
Picking the best route for order pickers
The routes that pickers in warehouses take are essential to efficiency. But which route is best?
What is the chance of throwing six with a fair die?

If, after reading the title, your immediate response is to shout "1/6-th", then you have correctly answered the question. Well done! However, in this article we will focus on the meaning of this question. What exactly is this "chance" of which you've just exclaimed it equals 1/6-th?
Urban nature: decoding connectivity with networks

Rapid urbanization without consideration for the environment is currently threatening urban dwellers. Its effects are exacerbating climate change and the urgency to adapt to our circumstances is growing. Network science may just have the key to solving our multifaceted problems.
