Cycling to 57,912 National Monuments in the Netherlands
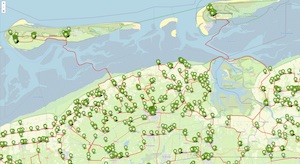
In March 2021 the largest roadmap instance of the traveling salesman problem ever was solved. This is a new record for the Travelling Salesman!
Discussing with two great mathematicians

Before the summer break we interviewed together with Raf Bocklandt mathematicians David Aldous and László Lovász.
A big breakthrough in the Euclidean Travelling Salesman Problem
Recently there has been a breakthrough in the field of algorithms for geometric network problems, concerning the complexity of the Euclidean Travelling Salesman Problem.
Sociomaths: The maths of living apart together

Phenomena like social cohesion and polarisation emerge from individual interactions on the social network of relationships between people. So, what does this network look like?
DNA self-assembly gives birth to new mathematics
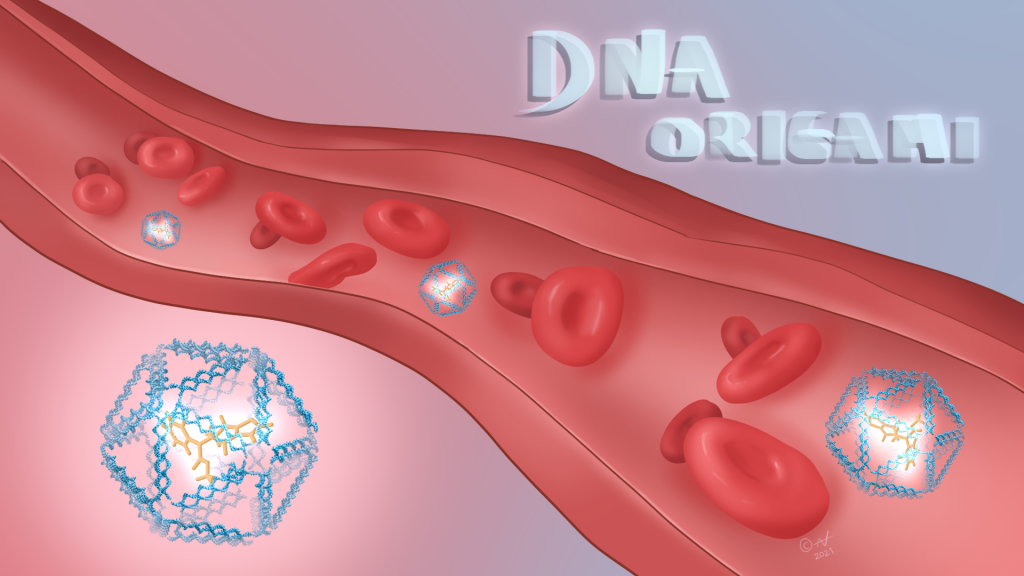
At this very moment, the emergent science of DNA self-assembly is giving birth to a new field of mathematics that might be called DNA-mathematics. Cleverly constructed DNA molecules will self-assemble into pre-determined complex structures when placed in solution together.
Not all jet-lags are the same

The part of the brain that controls the sleeping cycle is made up of two groups of neurons. In order for you to be able to sleep at night, the activity of these neurons needs to be synchronized with the cycle of the sun (e.g. active during the day and inactive at night). When you abruptly change the cycle of the sun (by flying to New York) these two groups need to re-synchronize to the new sun-cycle.
Gödel's incompleteness theorem in 15 minutes?

Is it possible to fully understand Gödel's incompleteness theorem in 15 minutes?
Predicting optimal routes in unpredictable networks
How does your navigation system find the fastest route in a road network, if it does not know where traffic jams occur and how long they last?
Words of Women in Mathematics in times of Corona

The common narrative at the beginning of the pandemic last year, prompted by the global scale of the crisis, was that we were all on the same boat. Of course, we quickly realized that was not the case.
Passing a negative coin

A brand new solution to an old mathematical problem. This time we found it by throwing in some negative cash, the debt.
