Random Graphs and Complex Networks: Volume 2 has appeared!
In February 2024, the second Volume of the Random Graphs and Complex Networks book series has appeared. This volume is aimed more towards the research community, including PhD students and researchers, with a mathematical background.
ICTS-NETWORKS workshop: A Confluence of Ideas
In the vibrant city of Bangalore, India, the International Centre for Theoretical Sciences (ICTS) played host to a discussion meeting titled "Challenges in Networks" from January 29 to February 2, 2024.
The Mysterious R explained in simple terms
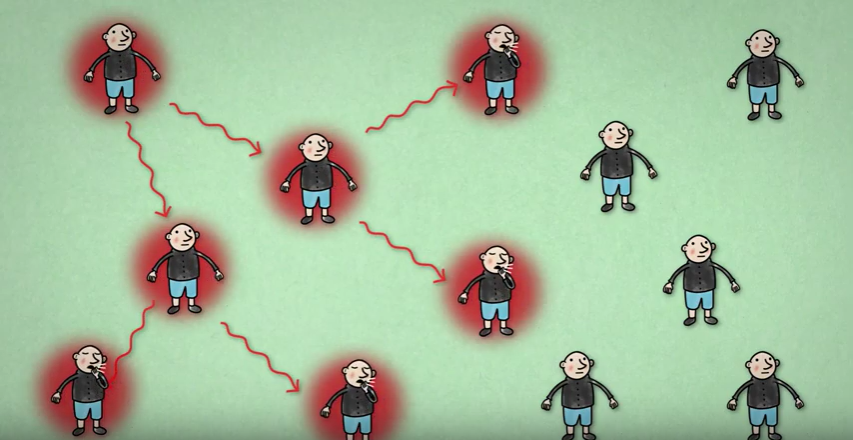
During the Corona pandemic the reproduction number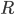 
appeared in much of the media. While it is not at all obvious what this quantity measures exactly, it is obvious that making it smaller than 1 really is crucial in controlling the spread of the virus. So what is this really?
How the popular become even more popular
Many networks, from technological to social networks, and from the world-wide web to collaboration networks, have a hub-like structure. Why is this the case, and why are they not much more homogeneous?
Degrees in graphs IV: degrees in large real-world networks
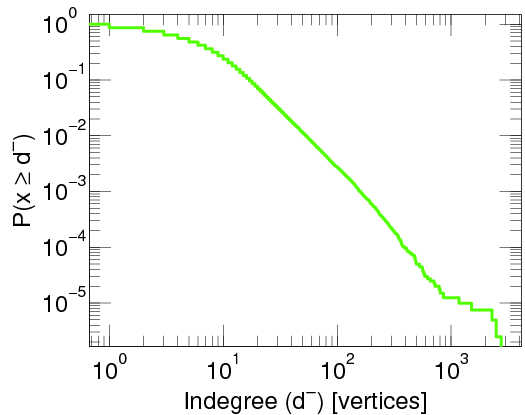
How are elements in real-world networks connected? That is the question we aim to answer in this post. Most real-world networks turn out to be extremely inhomogeneous.
Degrees in graphs III: Which degrees sequences are possible?
Paul Erdős and Tibor Gallai developed a beautiful criterion to decide precisely when a degree sequence is graphical.
Degrees in graphs II: Degree sequences
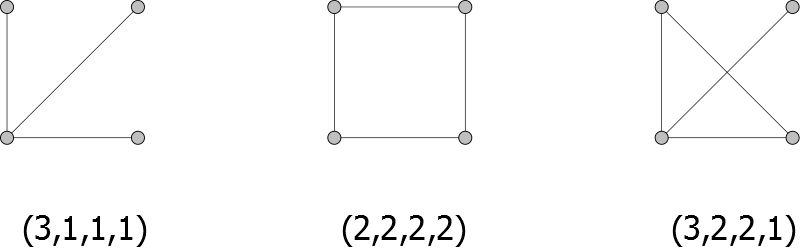
The degree sequence of a graph is the sequence of degrees of all its elements.
After a long wait: book `Random Graphs and Complex Networks' appeared
Written for the course `Random Graphs' at Eindhoven University of Technology, and class room tested for over ten years, the book `Random Graphs and Complex Networks' has now finally appeared in print at Cambridge University Press.
Degrees in graphs I: the Handshake Lemma
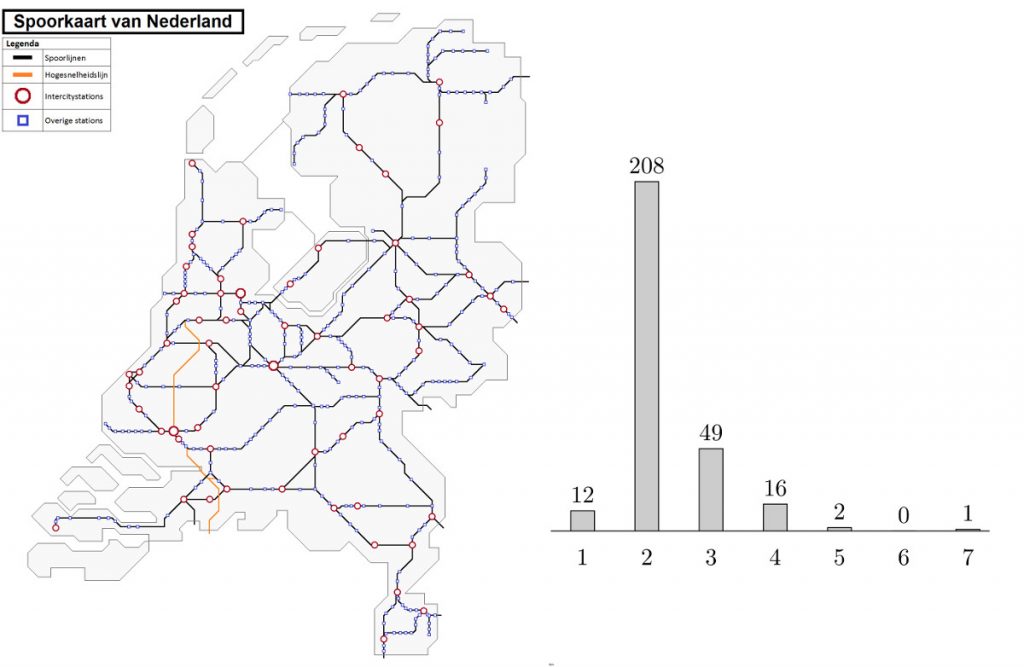
A graph consists of objects called vertices and connections between them called edges. For every vertex, we can count how many neighbors it has, which is called its degree.
Stella Kapodistria wins contest `Network Pages'
The Networks Pages proudly presents the winner of the first Network Pages contest for the best logo, wordart image or artistic network photo: Stella Kapodistria.