Euler's formule voor veelvlakken
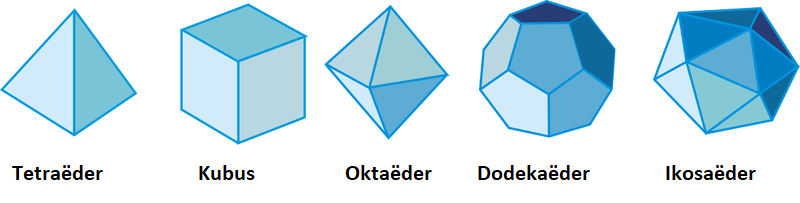
We beschouwen een convex veelvlak. Een veelvlak is een drie dimensionaal meetkundig object dat samengesteld wordt door een eindig aantal congruente veelhoeken. Voorbeelden van convexe veelvlakken zijn de kubus, de viervlak, de vierzijdige pyramide, enzovoort.
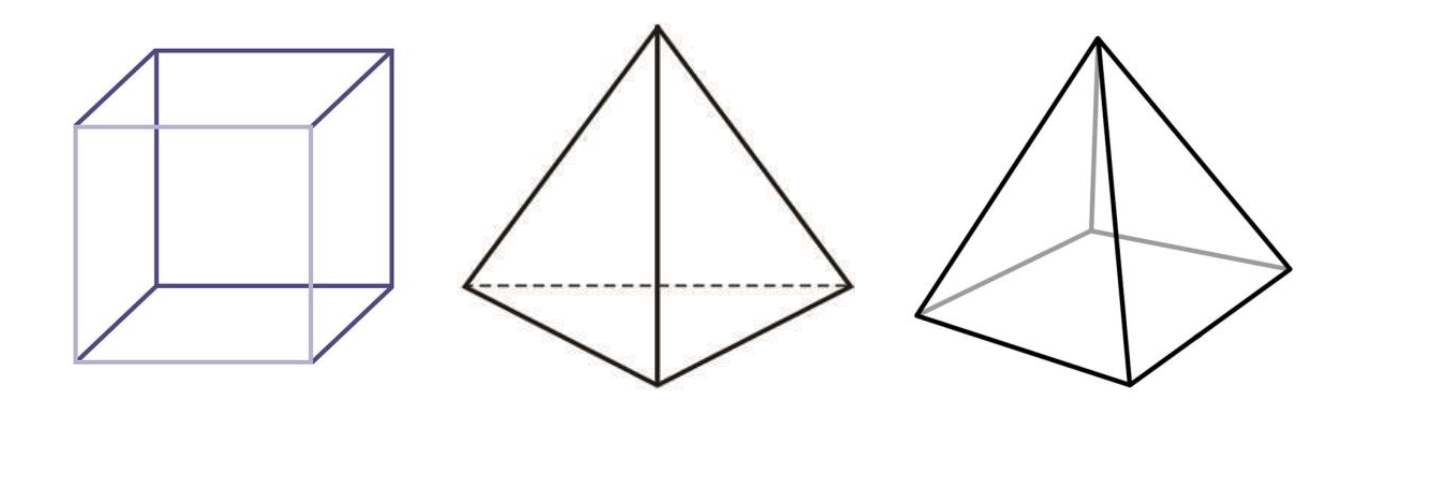
We noemen een veelvlak convex als het aan de volgende eis voldoet, neem twee willekeurige punten die op het veelvlak liggen en trek de rechte lijn die deze twee punten verbindt, dan ligt deze lijn in de inwendige (interieur?) van het veelvlak. De drie veelvlakken gegeven hierboven zijn allemaal convex. Een voorbeeld van een niet-convex veelvlak is de tetrahemihexahedron.

Een veelvlak wordt gebouwd door drie bouwstenen, een aantal hoekpunten (v), een aantal ribben (e) en een aantal zijvlakken (f). Voor elk veelvlak, convex of niet convex, zijn deze drie getallen goed gedefinieerd. Voor de voorbeelden boven deze karakteristieken worden gegeven in de volgende tabel
In mijn ogen is het niet vanzelfsprekend dat er een verband bestaat tussen deze drie bouwstenen van een veelvlak. In de achttiende eeuw heeft de wiskundige Leonard Euler de volgende formule ontdekt die een verbant legt tussen het aantal hoekpunten 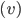 , het aantal ribben
, het aantal ribben 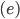 en het aantal zijvlakken
en het aantal zijvlakken 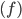 in een convex veelvlak
in een convex veelvlak
\begin{equation}\label{Euler}v-e+f = 2. \end{equation}
En wat zo magisch is, is dat deze formule geldt in alle convexe veelvlakken! Neem bijvoorbeeld de kubus, dan volgens de bovenstaande tabel 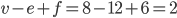 , in de veervlak en de pyramide komt ook precies 2 uit. Ga ook zelf aan de slag, neem een ander convex veelvlak en verifieer dat
, in de veervlak en de pyramide komt ook precies 2 uit. Ga ook zelf aan de slag, neem een ander convex veelvlak en verifieer dat 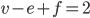 . Let op, je veelvlak moet convex zijn, er mogen geen gatten er in zitten en ook geen stekels er uit steken! In de tetrahemihexahedron we zien bijvoorbeeld dat
. Let op, je veelvlak moet convex zijn, er mogen geen gatten er in zitten en ook geen stekels er uit steken! In de tetrahemihexahedron we zien bijvoorbeeld dat 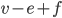 gelijk is aan 1.
gelijk is aan 1.
En nu de essentie van dit artikel, we hebben deze formule verifieerd voor drie gevallen van convexe veelvlakken maar hoe kunnen we laten zien dat die geldt in alle convexe veelvlakken? Is het misschien mogelijk om een ingewikkeld veelvlak te construeren dat convex is en tegelijkertijd niet aan deze formule voldoet? Laten even kijken waarom dat niet mogelijk is.
Het bewijs we gaan bespreken, bedacht door de wiskundige Augustin-Louis Cauchy in 1811, maakt gebruik van Schlegel diagrammen, die zijn graaf-representaties van een convex veelvlak op het platte vlak. Dit bewijs legt een verband tussen twee grote onderdelen van de wiskunde, de meer klassieke onderdeel van de meetkunde, en de meer moderne onderdeel van het grafentheorie. Het idee is dat als we een veelvlak gaan projecteren op het platte vlak dan krijgen we een graaf, deze graaf heet de Schlegel diagram van het veelvlak. Laten we kijken hoe dit werkt met een paar voorbeelden.
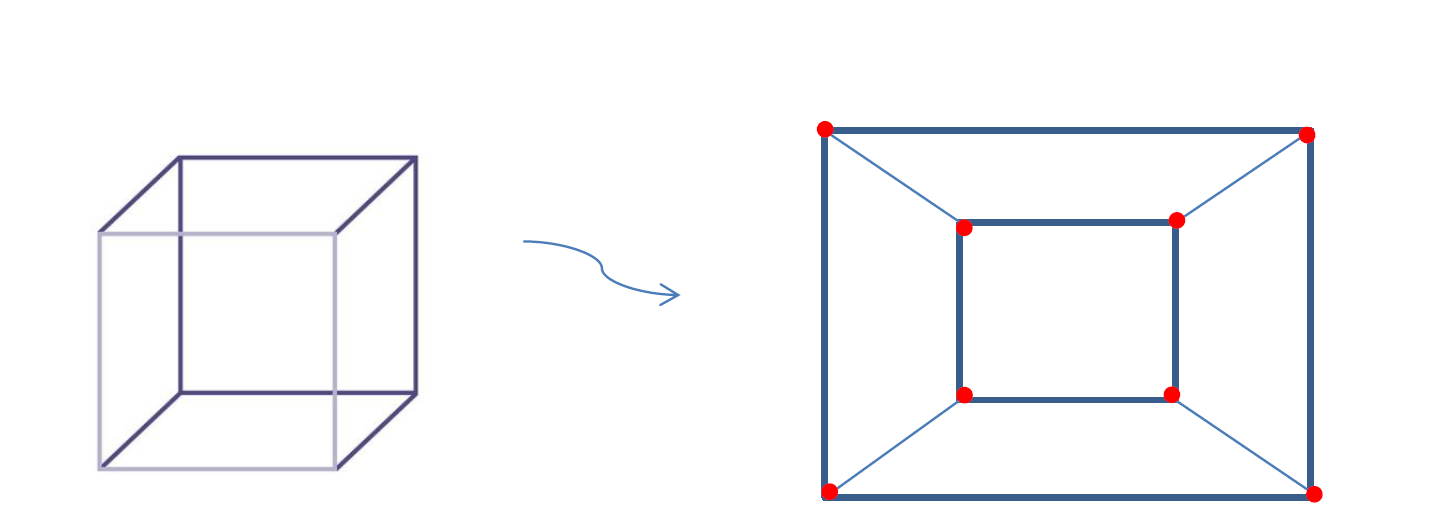
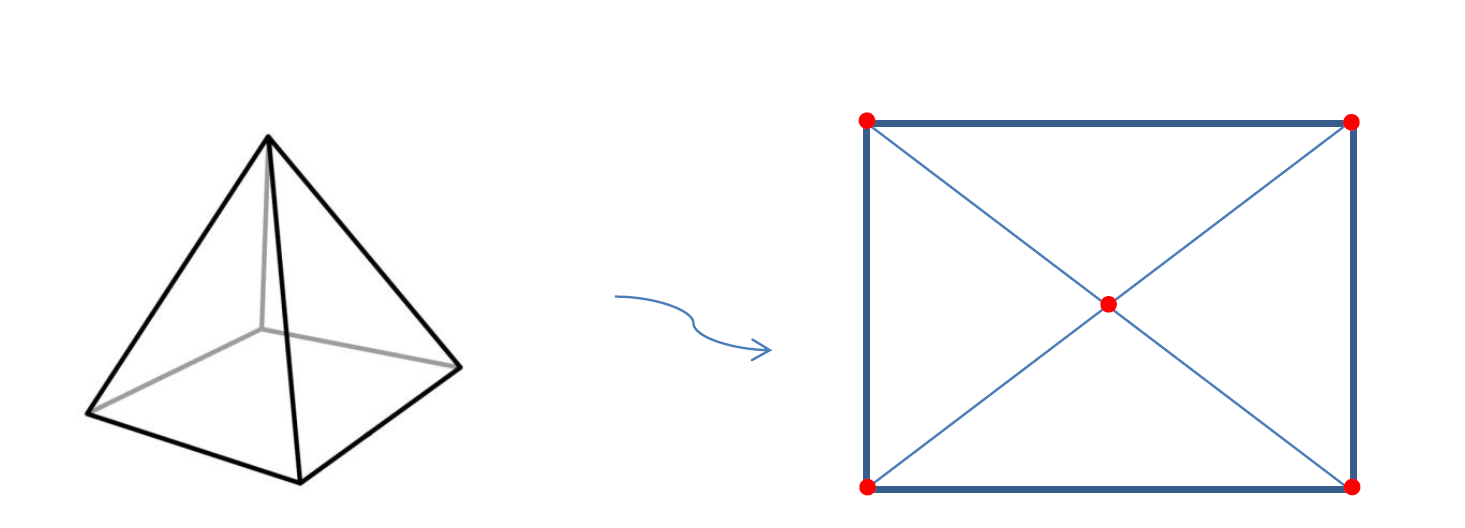
Deze graaf heeft twee belangrijke eigenschappen. Ten eerste hij heeft hetzelfde aantal punten en zijden zoals het oorspronkelijke veelvlak en heeft één zijvlak minder. De tweede eigenschap is dat hij is plenair, dat betekend dat geen twee zijden elkaar snijden. Dus om Euler’s formule te bewijzen voor een convexe veelvlak het is voldoende om te bewijzen dat in een plenaire graaf de volgende formule geldt
\begin{equation}\label{Euler2}v-e+f =1.\end{equation}
We hebben dus een meetkundige probleem vertaald naar een graaf-theoretische probleem! Dat is zo mooi met de wiskunde, dat je soms naar een andere wereld mag rijzen om iets te bewijzen! We gaan dus verder met het bewijs voor plenaire grafen.
We beschouwen een plenaire gaaf. Het idee is dat we deze graaf gaan transformeren, door midden van operaties op de zijvlakken, naar een eenvoudiger graaf op zo’n manier zodat de linke kant van \eqerf{Euler2} invariant blijft. De twee operaties we gaan toepassen op de graaf zijn de volgende:
Operatie 1: Zoek in de graaf een zijvlak die “kijkt” naar meer dan drie punten. We verbinden twee van deze punten. Dan krijgen we een nieuwe zijde in de graaf en twee zijvlakken in plaats van één. Dus in de nieuwe graaf 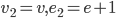 en
en 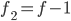 , en
, en 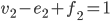 . Dus
. Dus 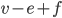 blijft dezelfde en bovendien de graaf is nog steeds plenair. We herhalen deze procedure tot dat het niet meer kan. Aan het einde krijgen we een graaf die wordt gebouwd door veel driehoeken, misschien met gekromde zijden maar dit maakt niet uit voor het bewijs.
blijft dezelfde en bovendien de graaf is nog steeds plenair. We herhalen deze procedure tot dat het niet meer kan. Aan het einde krijgen we een graaf die wordt gebouwd door veel driehoeken, misschien met gekromde zijden maar dit maakt niet uit voor het bewijs.
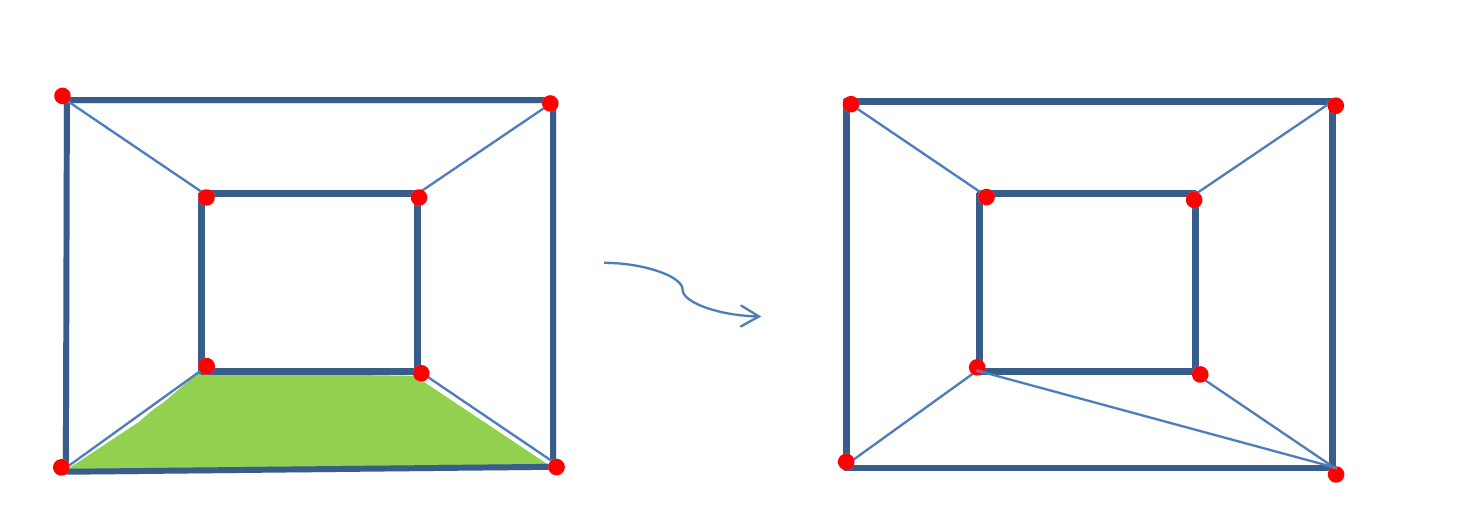
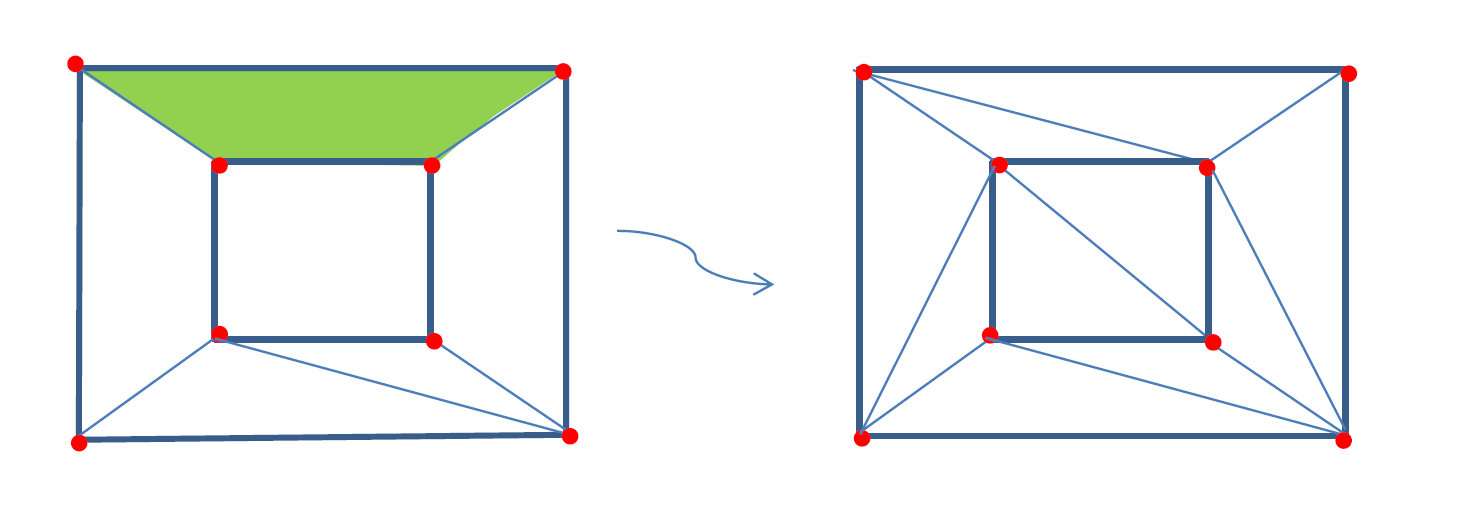
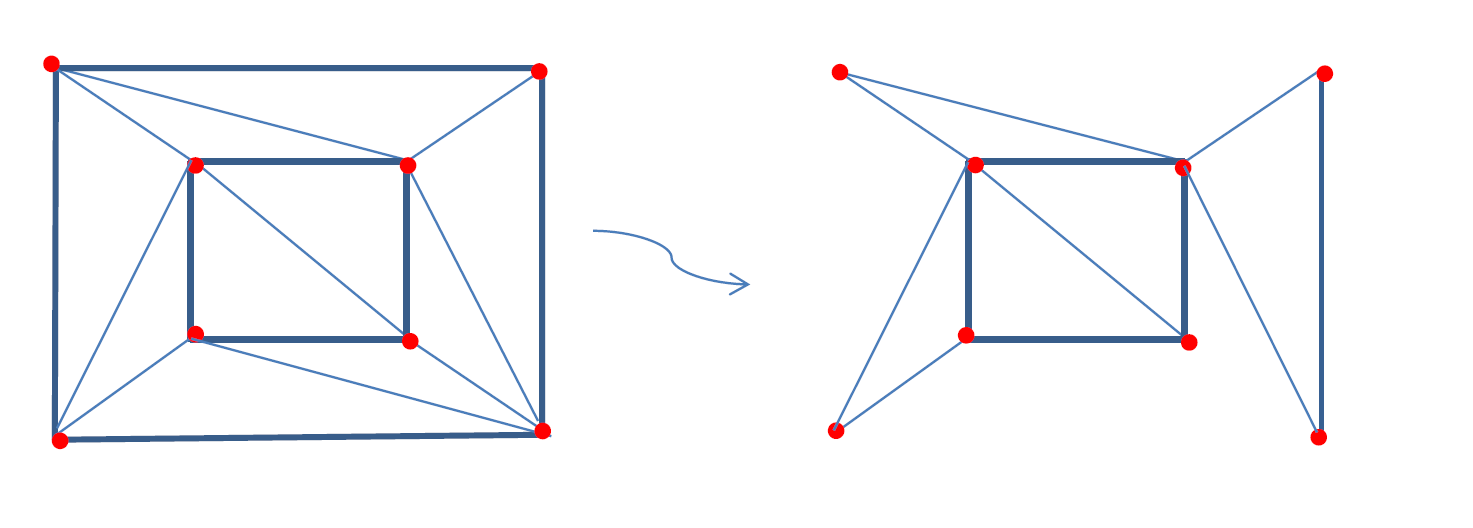
Operatie 2: De tweede operatie heeft als doel om zijvlakken te verwijderen onder de voorwaarde dat v-e+f invariant blijft. In onze graaf elke zijvlak kan 0,1,2 of 3 gezamenlijke zijden hebben met het buitenvlak van de graaf. We verwijderen een zijde die één gezamenlijke zijde heeft met het buitenvlak. Dan verdwijnt één zijde en één vlak en dus de formule blijft invariant. We herhalen deze procedure tot dat het niet meer kan, vervolgens gaan we zijvlakken verwijderen die twee gezamenlijke zijdes hebben met het buitenvlak. Uiteindelijk hebben we een graaf die wordt samengesteld door disjuncte driehoeken, en voor driehoeken we weten dat de formule geldt! Quod erat demonstrandum!
We hebben dus bewezen dat in elk convex veelvlak geldt dat 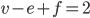 . We hebben ook een voorbeeld van een niet-convex veelvlak, namelijk de tetrahemihexahedron, waarvoor deze formule niet geldt. Dus de formule geldt niet voor alle veelvlakken. Maar is convexiteit ook noodzakelijk? Zijn er niet convexe veelvlakken waarvoor de desbetreffende formule wel geldt? Het antwoord is ja! Neem bijvoorbeeld een kubus met een kleinere pyramide boven op! (Opgave: Maak een plaatje en laat zien dat
. We hebben ook een voorbeeld van een niet-convex veelvlak, namelijk de tetrahemihexahedron, waarvoor deze formule niet geldt. Dus de formule geldt niet voor alle veelvlakken. Maar is convexiteit ook noodzakelijk? Zijn er niet convexe veelvlakken waarvoor de desbetreffende formule wel geldt? Het antwoord is ja! Neem bijvoorbeeld een kubus met een kleinere pyramide boven op! (Opgave: Maak een plaatje en laat zien dat 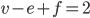 ). Kunnen we dit verklaren? In het bewijs we hebben eigenlijk een sterker resultaat bewezen, namelijk dat in elke plenaire graaf geldt dat
). Kunnen we dit verklaren? In het bewijs we hebben eigenlijk een sterker resultaat bewezen, namelijk dat in elke plenaire graaf geldt dat 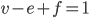 . Laten we het Schlegel diagram van dit veelvlak gaan tekenen, het is een plenaire graaf! (Opgave)
. Laten we het Schlegel diagram van dit veelvlak gaan tekenen, het is een plenaire graaf! (Opgave)
De platonische lichamen
Een platonisch lichaam, of anders een canoniek veelvlak, is een veelvlak waar elke zijvlak een canoniek veelhoek is. Een voorbeeld van een canoniek veelvlak is de kubus, elke zijvlak is een vierkant. Veel interessante vragen komen nu opdagen. Welke andere canonieke veelvlakken bestaan? En hoeveel zijn deze? Kan ik met elke regulier veelhoek een regulier veelvlak maken? Laten we deze vraag gaan onderzoeken! Ten eerste bij elke veelvlak er correspondeert een unieke drieling getallen 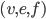 , vanwege de formule van Euler in \eqref{Euler}. Maar gegeven een
, vanwege de formule van Euler in \eqref{Euler}. Maar gegeven een 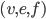 het is niet zo makkelijk te zien wat voor veelvlak hij representeert. Bijvoorbeeld kun je zien welke veelvlak
het is niet zo makkelijk te zien wat voor veelvlak hij representeert. Bijvoorbeeld kun je zien welke veelvlak 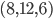 representeert? Het is de kubus maar het is niet zo makkelijk te zien in eerst instantie. Het is meer inzichtelijk om te weten hoe veel zijvlakken elkaar treffen op elke punt, deze noteren we met
representeert? Het is de kubus maar het is niet zo makkelijk te zien in eerst instantie. Het is meer inzichtelijk om te weten hoe veel zijvlakken elkaar treffen op elke punt, deze noteren we met 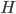 , en hoeveel ribben elke zijvlak heeft, deze noteren we met
, en hoeveel ribben elke zijvlak heeft, deze noteren we met 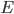 . Voor de kubus bijvoorbeeld
. Voor de kubus bijvoorbeeld 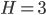 en
en 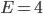 , dus 3 vierkanten treffen elkaar op elk punt. Beschouw een canoniek veelvlak en kijk naar alle zijvlakken los van elkaar. Dan krijg je
, dus 3 vierkanten treffen elkaar op elk punt. Beschouw een canoniek veelvlak en kijk naar alle zijvlakken los van elkaar. Dan krijg je 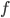 veelhoeken met totaal
veelhoeken met totaal 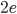 ribben en
ribben en 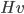 punten. Dit leidt tot de vergelijking
punten. Dit leidt tot de vergelijking
\begin{equation}\label{EulerE1}Hv = fe.\end{equation}
Met een vergelijkbare redenering krijgen we ook de vergelijking
\begin{equation}\label{EulerE2}Ef= 2e.\end{equation}
Als we deze twee vergelijkingen gaan combineren met Euler’s formule dan krijgen we de vergelijking
\begin{equation}\frac{1}{H} + \frac{1}{E} – \frac{1}{2}= \frac{1}{e} \end{equation}
en dus 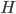 en
en 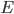 moeten voldoen aan de volgende ongelijkheid
moeten voldoen aan de volgende ongelijkheid
\begin{equation}\frac{1}{H} + \frac{1}{E} -\frac{1}{2}> 0.\end{equation}
Tegelijkertijd 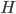 moet ook groter zijn dan 3, om een drie dimensionaal veelvlak te hebben. Naarmate
moet ook groter zijn dan 3, om een drie dimensionaal veelvlak te hebben. Naarmate 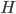 en
en 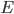 groeien, wordt
groeien, wordt 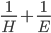 kleiner, dus we verwachten dat voor
kleiner, dus we verwachten dat voor 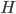 en
en 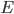 groot genoeg
groot genoeg 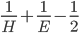 negatief wordt. Dus de vraag is hoe groot moeten
negatief wordt. Dus de vraag is hoe groot moeten 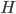 en
en 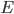 zijn? De resultaten zijn in de volgende tabel gegeven
zijn? De resultaten zijn in de volgende tabel gegeven
De conclusie is dat er bestaan precies vijf canonieke veelvlakken, ook de vijf platonische lichamen genoemd. Die zijn de tetraëder (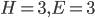 ), de kubus (
), de kubus (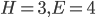 ), de octaëder (
), de octaëder (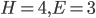 ), de dodecaëder (
), de dodecaëder (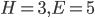 ) en de icosaëder (
) en de icosaëder (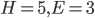 ).
).
Een voetbal
Heb je ooit een voetbal goed bekeken. Een voetbal is niet echt een bal, zoals we het ook noemen. De oppervlak van een voetbal wordt eigenlijk samengesteld door twee soorten veelhoeken, vijfhoeken en zeshoeken. Die hebben allemaal ook een beetje kromming natuurlijk zodat de voetbal kan makkelijk rollen. Stel dat er 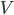 vijfhoeken zijn en
vijfhoeken zijn en 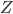 zeshoeken. Dan Euler’s formule levert de volgende vergelijking
zeshoeken. Dan Euler’s formule levert de volgende vergelijking
\begin{equation} \frac{5V+6Z}{3} - \frac{5V+6Z}{2} + V+Z = 2.\end{equation}
Als we de berekeningen gaan doen dan vinden we dat op een voetbal er zijn altijd 12 vijfhoeken! Maar wat gebeurt er met de zeshoeken dan? Ga zelf aan de slag om dit verder te onderzoeken!