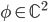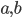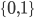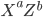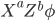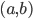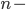During the last decades, many resources have been invested in quantum computing. This research field has grown immensely and amazing results have been obtained. The plans for the future are highly ambitious, but at the same time, there are serious questions that need to be addressed. Who will possess these quantum computers? How will they be used in practice? How can we safely encrypt information? Many scientists are working on these questions.
In January 2021 Yfke Dulek from the CWI and QuSoft, the Dutch research centre for quantum software, successfully defended her PhD thesis with the title Delegated and Distributed Quantum Computation. Yfke carried out her research under the supervision of dr. Christian Schaffner (UvA and CWI) and Prof. dr. Harry Buhrman (UvA, QuSoft). In this article some aspects of Yfke's work are presented without going into the technical details.

Yfke Dulek, photo taken from the website of the CWI.
In classical cryptography, the goal is to develop methods to encrypt classical messages. Classical here refers to messages consisting of binary bits, the building block of classical information.
Quantum computers perform computations using quantum bits, or qubits, and not classical bits. This means that quantum messages are inherently different from classical messages, while a classical message is usually modelled as a string of bits (0 or 1), a quantum message consists of qubits, much richer objects that can be in one of infinitely many different states. You can watch this very informative video made by Veritasium if you want to see in more detail how qubits work.
For the purposes of this article it is not very important to know more about how qubits work, just keep in mind that qubits have a much richer structure than classical bits.
In her dissertation, Yfke explored the power and limitations of cryptography for quantum data. Is it possible to securely delegate or distribute a quantum computation in a network of computers? Before diving into the quantum world and the details of Yfke’s research, let’s have a quick look at some important concepts from classical cryptography.
Quantum computing is a rapidly-emerging technology that harnesses the laws of quantum mechanics to solve problems too complex for classical computers.
IBM Quantum
Absolute security
The quest for safe encryption methods dates to ancient times, from the Scytale of the Spartans to the Ceasar cipher of the Romans. However, theoretically understanding how to construct a safe encryption mechanism is a much more recent endeavor. In 1883, Auguste Kerckhoffs observed that a proper secret key is crucial to a successful cryptographic protocol. Simply said, he postulated that an encryption should stay secure, if even everything about the encryption protocol, except of the secret key, is accessible to the public. Kerckhoffs’s principle has been essential to shaping cryptography as we know it today.
In 1948 Claude Shannon published his article “A mathematical theory of communication” which gave birth to the field of information theory. In his article, Shannon formalized the notion of information content of a message and showed that we can quantify information using bits that we can study mathematically.
To properly hide a message from adversaries, one has to ensure that there is no information about the message present in the ciphertext, the text we obtain after encrypting the message. At the same time, a receiver who knows the secret key should of course be able to decipher all the information about the message. Shannon showed that the only way to simultaneously achieve these properties is to use a secret key of the same length as the message.

Claude Shannon, photo taken from Wikipedia.
The canonical example of an information-theoretically secure encryption scheme is the one-time pad. Encrypting an  -bit message
-bit message  , say for example
, say for example  (
( ), requires an
), requires an  -bit secret key
-bit secret key 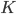 , say for example
, say for example 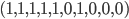 . The ciphertext
. The ciphertext  is is defined by simply taking the bitwise XOR between the message and the key:
is is defined by simply taking the bitwise XOR between the message and the key: 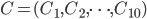 , where
, where 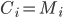 XOR
XOR 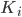 . The XOR operation gives 0 if
. The XOR operation gives 0 if 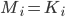 and 1 if
and 1 if 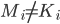 . We leave it as a puzzle for the reader to find the ciphertext
. We leave it as a puzzle for the reader to find the ciphertext 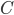 in the example above.
in the example above.
Absolute security may not be desirable
The one-time pad described above offers absolute security but in practical applications it may not be desirable. For every encrypted message that has to be communicated, a secret key of the same length should also be communicated. This renders the one-time pad rather inefficient. Hence we see that a balance between security and efficiency is desirable.
Public-key cryptography, where messages are encrypted using a key that is publicly known, and are decrypted with a private key which is known only to the decrypting party, reduces the amount of information that needs to be communicated. This is achieved by slightly relaxing what it means to keep a message secret: instead of requiring that the ciphertext contains no information about the message, it is only required that the information is hard to retrieve. This idea is usually formalized by stating that if one is able to recover the message from the ciphertext, then one is also able to solve a specified mathematical problem.
Examples of such problems that are used in cryptographic systems are integer factorization or discrete logarithms of elliptic curves. Under the assumption that this mathematical problem is hard to solve, it should be practically impossible to break the encryption. This provides both efficiency for the user and computational intractability for the attacker. The same ideas hold also in the world of quantum computers for the encryption of quantum messages. Cryptographic systems are based on problems which are believed not to be easily solvable by a quantum computer.
The quantum shield
As described above, classical encryption protocols rely on mathematical problems that are believed to be difficult to solve. Quantum encryption protocols rely on the same idea, but the important question is whether mathematical problems that are classically difficult are also quantumly difficult. In any case, this does not hold for integer factorization.
In 1994 Peter Shor discovered a quantum algorithm that can solve prime factorization in polynomial time. At the same time, it is still not known whether there is a classical algorithm that can solve prime factorization for large numbers in polynomial time. Hence encryption algorithms that rely on prime factorization are not secure against an attack from a quantum computer. A notable example of an information-theoretically secure quantum protocol is the quantum one-time pad, which securely encrypts quantum messages.
Similarly to the classical one-time pad, the secret key for the quantum one-time pad is fairly large: to encrypt a message consisting of  qubits, one needs a secret key of length
qubits, one needs a secret key of length 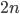 . The crucial fact that makes the quantum one-time pad a useful tool, however, is the fact that the secret key can consist of classical bits! Since qubits are very sensitive and unstable, using classical keys makes life much easier, even if their length is twice the length of the quantum message. To understand how the quantum one-time pad works we need a little bit of linear algebra. The interested reader can click on the extra explanation below, otherwise just keep reading, these mathematical details are not needed in the rest of the article.
. The crucial fact that makes the quantum one-time pad a useful tool, however, is the fact that the secret key can consist of classical bits! Since qubits are very sensitive and unstable, using classical keys makes life much easier, even if their length is twice the length of the quantum message. To understand how the quantum one-time pad works we need a little bit of linear algebra. The interested reader can click on the extra explanation below, otherwise just keep reading, these mathematical details are not needed in the rest of the article.

Peter Shor, photo taken from Wikipedia.
Distributing and delegating qubits
In her research Yfke focussed on another complication that emerges due to the nature of quantum computers. Functional quantum computers are very sensitive and delicate machines, which means that when they will become available for open public use, they will likely be in possession of large institutions, either companies or universities, that can guarantee for their proper functioning. Users can then log on and use the quantum computer for their needs. This means that quantum computations will most likely be distributed amongst multiple parties, or delegated to a party that has possession of a quantum computer. It is thus important that quantum encryption protocols take distribution and delegation of information into consideration. In her PhD Yfke explored the possibilities, and impossibilities, of various cryptographic primitives, the building blocks of encryption protocols, for delegated and distributed quantum computation. Specifically, Yfke considered three quantum-cryptographic primitives, namely quantum homomorphic encryption, multi-party quantum computation and quantum obfuscation.
Fully Homomorphic Encryption
The discovery of fully homomorphic encryption (FHE) in classical cryptography in 2009, is widely considered to be one of the major breakthroughs of the field. Unlike standard encryption, FHE makes it possible for parties that do not hold the decryption key to perform computations on encrypted data.
In this method encrypting a message corresponds to applying an homomorphism on the plaintexts, mapping them into the ciphertext.
Homomorphism In mathematics a homomorphism is a map 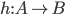 between two sets
between two sets 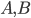 , which are equiped with the same structure, that preserves the operations defined on
, which are equiped with the same structure, that preserves the operations defined on 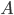 and
and 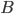 . For example, if
. For example, if 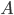 and
and 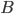 are the sets of integer numbers
are the sets of integer numbers 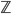 with addition as an operation, then the map \begin{equation} h(k) = 2\cdot k \text{ }(= k+k) \end{equation} is a homomorphism because
with addition as an operation, then the map \begin{equation} h(k) = 2\cdot k \text{ }(= k+k) \end{equation} is a homomorphism because 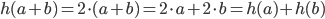 . But if we consider multiplication instead of addition, then this
. But if we consider multiplication instead of addition, then this 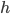 is not a homomorphism, since
is not a homomorphism, since 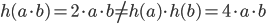 . Hence a homomorphism preserves the operation.
. Hence a homomorphism preserves the operation.
Hence, as the explanation above suggests, performing operations on the plaintexts should be preserved after applying such a homomorphism. This property allows parties to perform computations on the encrypted data. Decryption corresponds to inverting the homomorphism.
The same idea applies also in quantum cryptography, but now operations are applied to qubits. In quantum homomorphic encryption (QHE), quantum input data is encrypted in such a way that a server can carry out arbitrary quantum computations on the encrypted data, without interacting with the encrypting party.
In her research, Yfke worked with a hybrid classical-quantum construction, based on a very natural idea: to encrypt a quantum message under the quantum one-time pad, and to encrypt the (classical) keys to the quantum one-time pad under classical FHE, attaching the ciphertexts to the quantum ciphertext. The construction of quantum homomorphic encryption raises an important question: do the numerous classical applications of FHE have suitable quantum analogs?
As it turns out, most of the classical applications require an additional property that is simple classically, but nontrivial quantumly. That property is verification: the ability of the user to check that the final ciphertext produced by the server is indeed the result of a particular computation, homomorphically applied to the initial user-generated ciphertext. In the classical case, this is a simple matter: the server makes a copy of each intermediate computation step and provides the user with all these copies. In the quantum case, such a “transcript” or “log” appears to violate the no-cloning principle!
Yfke constructed a new QHE scheme where the server can certify, using a classical computation log as “proof”, that a particular homomorphic computation was performed on a quantum ciphertext. The main idea is that some additional qubits are used during the quantum computation, so-called traps. These trap-qubits don’t contribute to the actual computation, their role is purely to yield information on whether the desired computation is performed correctly. During the computation, these trap-qubits will be measured at suitably chosen moments, where we can theoretically predict their state. If all the measurements of the trap-qubits agree with the outcomes that were predicted theoretically, we have a verification that the desired quantum computation was performed correctly!
The more personal aspect
Before we conclude this article we would like to give the word to the doctorate.
Yfke, would you like to share some memories with us?
“The final result of my thesis (about the impossibility of obfuscation) was very surprising to me. Obfuscation refers to encrypting the code of a (quantum) program, instead of an input value. A computer must be able to run the encrypted program but a user should not be able to retrieve the source code. It was already known to be impossible by using classical computers, but for a long time, it was believed that "quantum obfuscation" could exist. There were good reasons to believe this, given the nature of qubits, which rarely reveal all of the information stored in them. Surely, one could use those quantum states to encode information about a secret function? From the start of my PhD, I had been set on constructing such quantum obfuscation. I had ideas on how to do it, but every time, it seemed that some ingredient was still missing. This led to at least two other papers, which were interesting in their own right, but for me, they were mostly intermediate steps toward the ultimate goal of quantum obfuscation. As the deadline for my dissertation was approaching, I started to lose hope of ever constructing it. My advisor, who had been trying alongside me to construct this elusive cryptographic notion, suggested that maybe it was not possible after all and we should try to prove that. He was right: within a few weeks, we had the rough outline of an impossibility proof, just in time for this major result to be included in my thesis. Not exactly the result I had been aiming for, but the dissertation did feel a lot more complete with it.”
Were you also involved in some activities you would like to share with the readers?
“Because the field is still relatively young, and therefore still growing, there is a small international network of researchers who actively reach out to the younger members of the community. I have been given many opportunities to showcase my work, by being invited to speak at workshops and summer schools in Barbados, Canada, and Switzerland, among others. In the spring of 2020, I spent a semester at the Simons Institute for the Theory of Computing in Berkeley (California) as a fellow during one of their research programs, which always attracts many international visitors.”
Concluding
Yfke’s research focused on quantum cryptography, and more specifically, on cryptographic primitives for delegated and distributed quantum computation. She studied three quantum-cryptographic primitives, namely quantum homomorphic encryption, multi-party quantum computation and quantum obfuscation.
Currently Yfke is working as a postdoctoral researcher at QuSoft and the CWI, where she furthers her research on quantum cryptography. We wish Yfke all the best with her further research trying to make the quantum world a safe place to compute.
This article is a slightly adapted version of the original article written for the December issue of 2021 of the magazine Nieuw Archief voor Wiskunde. The featured image is made by Pete Linforth and taken from Pixabay