At this very moment, the emergent science of DNA self-assembly is giving birth to a new field of mathematics that might be called DNA-mathematics.
New areas of mathematics arise constantly, with advancing human endeavors demanding mathematical innovation in every epoch of history. The concerns of early times, such as land division, pyramids, censuses, and calendars led to enumeration and trigonometry. As cultures advanced, questions of architecture and navigation gave us geometry and the mathematics of static measurement. More recent history, with planetary motion, rocketry, and finance, led to calculus and the mathematics of motion in time and space.
All the resulting mathematics fields such as algebra, geometry, calculus, and statistics continue to grow and evolve. So does the world. What do we have in our world that did not exist in the times of Pingala, Pythagoras, al-Khwarizmi, and Zhu, in the times of Euler, Newton, and Leibniz? We have computers, cell phones, and the internet. We have food webs, social networks, and yes, the spread of covid-19. These modern problems gave rise to network and graph theory, the mathematics of interconnections. For example, graph drawing tools led to effective computer chip layouts and random graphs to modeling the worldwide web, with both areas then blossoming into highly active mathematics subfields. Right now, we can see the same phenomenon emerging from questions about shapes and interconnections driven by DNA nanotechnology.
Imagine shaking a bag full of magnets. They spontaneously join together to form a larger object. Now imagine that it is possible to specify not only the shape of the magnets, but also exactly which one can connect to which one and where. Carefully designing the individual shapes and where they connect will force a desired larger shape such as a star or cube to form when the bag is shaken. This is the basis of self-assembly. DNA self-assembly uses molecules as the shapes, and the Watson-Crick complementarity of sequences of bases to determine which molecules can connect to which and where. Cleverly constructed DNA molecules will self-assemble into pre-determined complex structures when placed in solution together.
Shapes made of DNA
In the 1980’s, Ned Seeman pioneered DNA self-assembly. He used DNA molecules called branched junction molecules that are shaped like starfish with anywhere from three to as many as 12 arms. These molecules can attach to one another via sequences of complementary DNA bases the ends of their arms, as though the starfish are holding hands. Thus, for example, six branched junction molecules with three arms each can join together to form the outline of a cube.
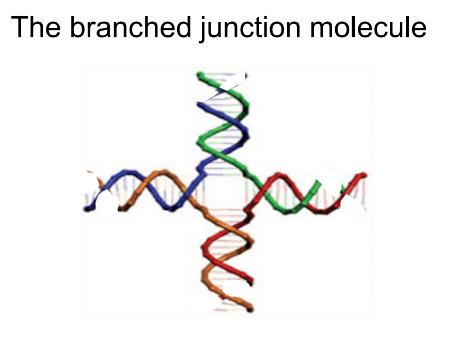
A four-armed branched junction molecule [1]
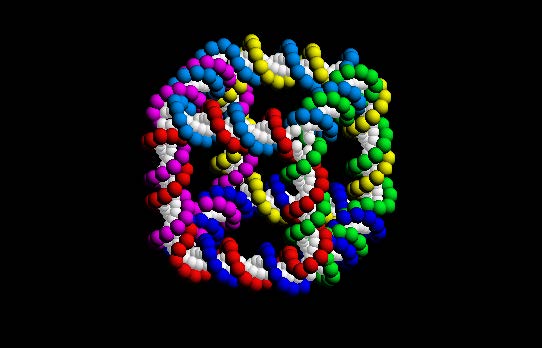
A cube self-assembled from DNA [2]
Then, in 2006, Paul Rothemund made a major advance in DNA self-assembly. He built tiny squares, triangles, and even smiley faces out of a long, single strand of DNA. This long strand of DNA self-assembles into a desired shape by filling it in with the help of about 200-250 short strands of DNA that fold and bind it into place. The long strand is called the scaffolding strand, and the short strands are aptly called staple strands. Think of the scaffolding strand as a long metal chain that fills in a desired shape by going back and forth, and the staple strands as little magnets each specially designed to stick together exactly two different segments along the chain. Due to the way the long strand of DNA folds in this process, this self-assembly method was dubbed ‘DNA origami’.
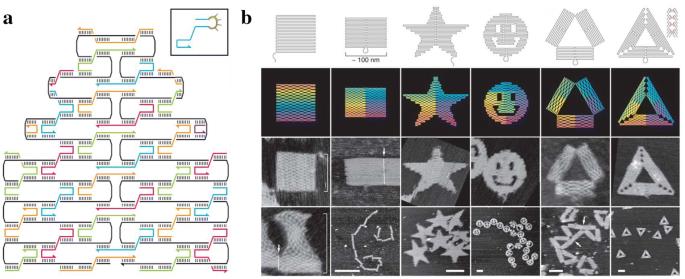
Wireframe DNA-origami
Because of the potential applications of self-assembling DNA nanotechnology, especially in medicine (watch this short video), and also in nanoscale robotics, circuitry, and biosensors, hundreds of laboratories around the world today focus on it. Scientists now use DNA self-assembly to produce 3D wireframe constructs as meshes and the outlines of polyhedra and, to demonstrate control over the process, even lacy snowflakes and bunny rabbits. They have also made nano-scale mechanical devices such as 40 nm boxes that open and close. If one of these boxes were the size of a pencil eraser, then a human would be the size of Belgium and the Netherlands together. Tiny containers such as these can carry nano-cargo such as blood clotting agents through the body, and may one day be used to treat disease.
Self-assembling DNA has potential in medicine. Illustration developed by Alex Nazlidis.
Designing DNA-origami
Scientists face many challenges in designing DNA molecules that will self-assemble into a desired shape. For example, if connected properly, four ‘L’ shapes can form a square. Unfortunately, if the wrong ends attach to one another, they might form into an undesired rectangle. Some of the design challenges involve chemical processes. Many others though involve structural questions such as which arms of the branched junction molecules should attach to which other arms, or how to route the scaffolding strand and staples through the desired structure, so that the smaller molecules then self-assemble into exactly the desired larger shape. Fortunately, problems involving shapes and interconnections are super exciting for mathematicians!
Thus, mathematicians have become natural collaborators with DNA self-assembly researchers and are now developing new mathematical formalism to solve mathematical problems arising from DNA self-assembly. Many of the target molecular shapes have wireframe structures, such as the outlines of a cube or octahedron. Since these outlines correspond to the edges of a graph and the corners of the shape to the vertices of a graph, graphs are excellent models for the assembly problems. However, existing graph theory cannot solve all the new problems arising from the self-assembly application, and so a new area of mathematics is born.
Here is just one example of the many problems comprising the new field of DNA-mathematics. Sometimes, after a shape has self-assembled, scientists want further information about it. For example, suppose several different types of branched junction molecules could self-assemble to form the outline of a cube in more than one way. A lab might lab hypothesize that certain experimental conditions determine which types of the branched junction molecules more readily form into the cube shape. If the lab performs an experiment with a particular set of conditions, it will then need to know which of the branched junction molecules actually appear in the final cube shape. One way to get that information is to extract a reporter strand from the cube. This is a strand of DNA that traces the whole shape, and thus ‘reports back’ on the molecules that comprise it. A reporter strand follows a route through the shape that traces every edge at least once, and if twice, then once in each direction (since DNA strands are directed from one end to the other). But is it even possible to find such a route for a reporter strand in any graph? If so, is it always possible to find an efficient route, i.e. to find the shortest possible route?
DNA-assembly problem
The goal is to extract a reporter strand from the DNA-structure. This is a strand of DNA that traces the whole shape, and thus ‘reports back’ on the molecules that comprise it. A reporter strand follows a route through the shape that traces every edge at least once, and if twice, then once in each direction.
Graph theory problem
Consider the graph representing the DNA-structure. Is it possible to find a route traversing all edges exactly once in each direction? More generally, is it possible to find such a route in any given graph?
Intuitively, suppose you have a pencil. Draw a graph. Can you, without lifting your pencil, trace over each of the edges at least once, and at most twice, and return to your starting point? If you trace over an edge twice, you must go in opposite directions. You also cannot go along an edge, turn around, and go immediately back along it.
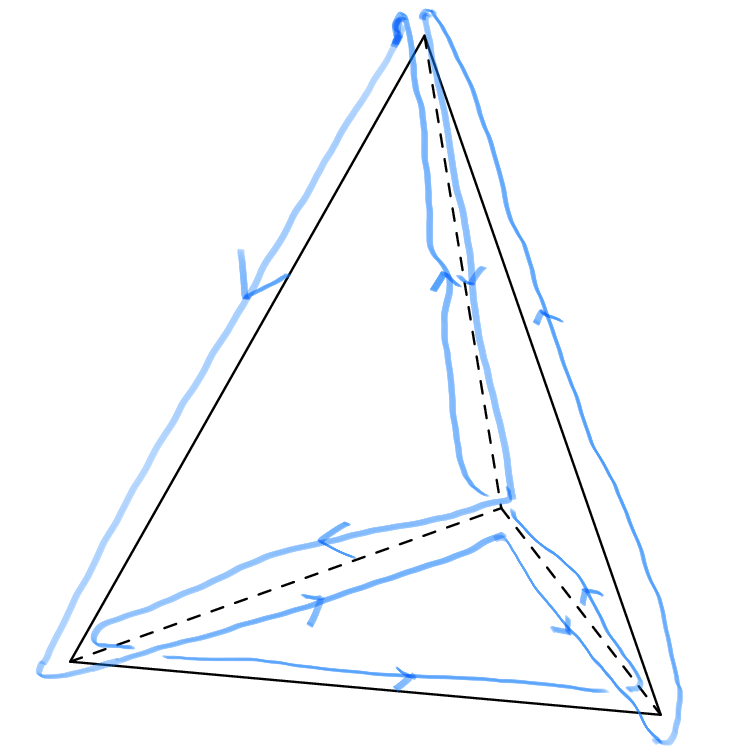
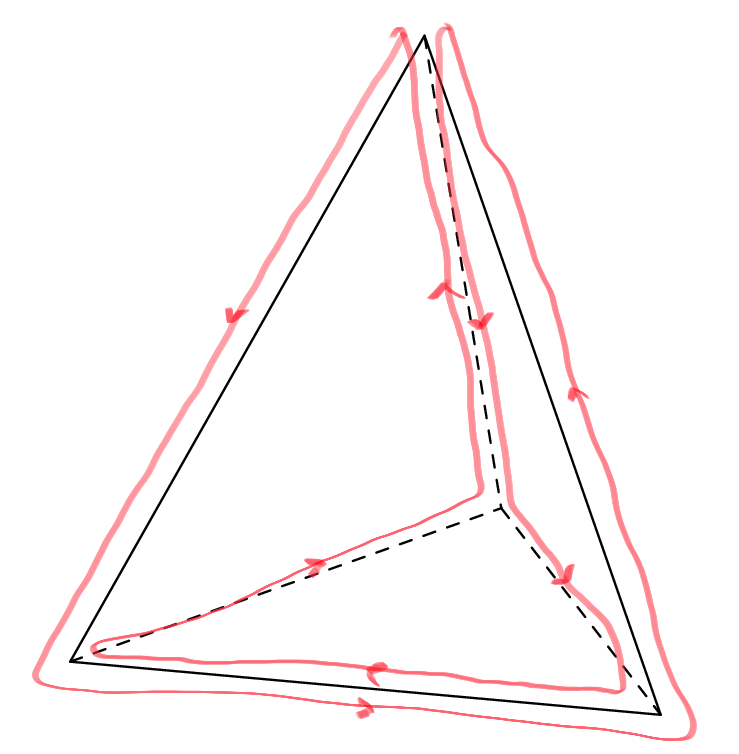
We observe that in both examples we traverse edges either once or twice, and if twice then once in each direction. So both routes are good solutions to the reporter strand problem. If we count, we see that the blue route traverses in total nine times the six edges while the red route eight. The red route is thus better since we want to find the shortest possible route. Can you do better than eight edges? If not, can you prove that the best route traverses eight edges? And try yourself to find a good reporter strand problem for the cube!
An unexpected connection
Mathematically, the most exciting aspects of this problem are the new research directions it opens in the area of topological graph theory. Topology graph theory involves drawing graphs on surfaces other than just the plane, for example on a torus, which has the shape of a donut. When a graph is drawn on a surface, the parts of the surface other than the edges and vertices of the graph are called the faces. For example, here is an example in Geogeof a cube viewed as a graph drawn on a sphere. Each square is one of the faces of the embedding of the cube graph on the sphere.
The problem of finding a route for a reporter strand is mathematically equivalent to asking: Is it possible to draw the graph of the desired shape on some surface (such as a sphere, torus, or double torus, etc.) so that all the edges go around one special face? There may be other faces as well, but there must be at least one face that all the edges lie on.
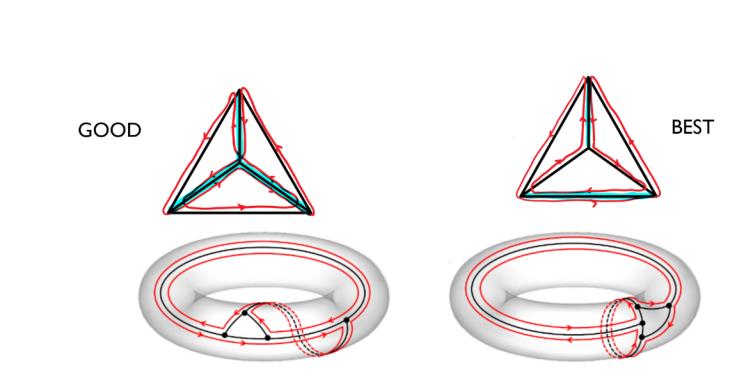
Drawing the two routes found for the tetrahedron on a torus using only the outer face. The graph splits the torus in two faces, one is the interior of the three points and the outer face.
Drawing graphs on surfaces is a fundamental area of research in topological graph theory. However, before this application, mathematical theory focused primarily on how many faces result from drawing a graph on a surface. This DNA assembly application directs attention to the sizes of special faces, something never previously investigated. We have devised a fast algorithm that always finds a route for a reporter strand through any graph. We also showed that it is NP-hard in general to find an shortest reporter strand route, meaning that the shortest reporter strand problem is at least as difficult as a large set of other problems for which no fast algorithms are known. Discovering that various DNA self-assembly problems are NP-hard is very interesting theoretically. Unfortunately, it does not help a lab trying to conduct its next experiment. Thus, we turn next to the whole host of consequent exciting problems that then arise, such as seeking approximation algorithms, finding optimal solutions for particular families of problems, and devising pragmatic approaches for urgently needed special cases. We often have to create new mathematical theory to address these problems. Moreover we are now seeking classes of graphs where it is possible to find these routes efficiently, and along the way, developing new theory and mathematical insights about graphs on surfaces. In turn, this new theory will fold back to inform the original question from the labs.
With many repeats of this pattern of mathematical discovery from DNA self-assembly problems, a new area of mathematics has been born. A significant applied problem such as DNA self-assembly launches novel mathematical investigations, as it demands innovative mathematical approaches and tools. The new area of mathematics not only informs the original problem, but also diverges from the initial stimulus to pursue problems of intrinsic mathematical interest which are independent of the application. This in turn opens rich new vistas of mathematics, taking the field in directions in might not have gone otherwise. Finally, the mathematical theories arising from the new-born field of DNA-mathematics become valuable design tools for lab scientists, further advancing the potential and capabilities of DNA self-assembly.
Rapid urbanization without consideration for the environment is currently threatening urban dwellers. Its effects are exacerbating climate change and the urgency to adapt to our circumstances is growing. Network science may just have the key to solving our multifaceted problems.
Between 1973 and 1986 multiple rapes and murders were committed in the state of California. Years later the idea was raised that these crimes might be connected. But traditional DNA analysis from the samples found at the crime scenes, could not identify the culprit.
Recently there has been a breakthrough in the field of algorithms for geometric network problems, concerning the complexity of the Euclidean Travelling Salesman Problem.
How can one hope to understand the precise structure of a virus if it is able to become unrecognizable within weeks? The mathematics behind this questions didn't let go of my mind for extensive periods of time during my PhD studies in Belgium.
