Enigma: Deductions from the menu

From this menu we can deduce some properties of the plugboard, and hopefully determine all the settings. For this, we first have to introduce some notation to make our life easier. Every time a letter is pressed on an Enigma machine, the internals of the machine change. We write 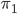$\pi_1$ for the permutation that encrypts the first letter, 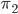$\pi_2$ the permutation that encrypts the second letter, etc. We also write a star after a permutation if we want to describe the setting of the machine 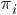$\pi_i$ without the plugboard.

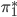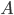For example, the permutation $\pi_1^*$ describes the permutation that decrypts the first letter of a message, but with the plugboard removed. To do deductions about the setting of the plugboard, we have to guess the setting of the rest of the machine. This seems like a big guess, but we will see later on that this won’t be an issue. We now hypothesize that $G$ and $A$ are connected on the plugboard.

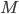We can see in the menu that $G$ is connected to $M$. We now try to deduce to what letter 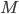$M$ is connected. All of the previous can be summarized in the following:

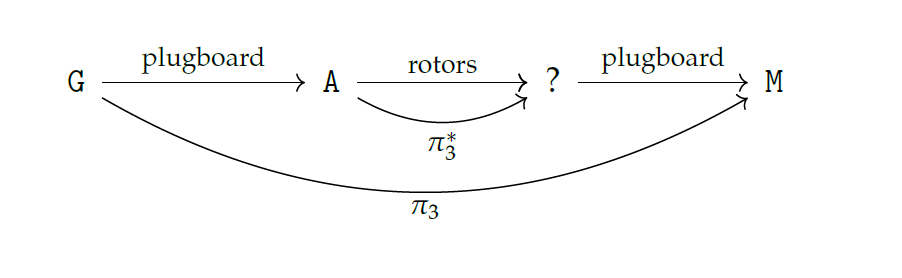
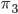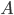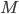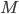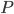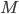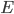From this, we can see that if we set up an Enigma machine with setting $\pi_3$ (the one we just guessed earlier), but omit the plugboard, we can simply press $A$ to see what letter $M$ is connected to on the plugboard. Let’s say, for example, that we find out that $M$ is connected to $P$ on the plugboard. Since $M$ and $E$ are connected on the menu, we can repeat the same procedure, but with 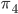$\pi_4$ instead of 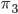$\pi_3$. This way, we can deduce to what letter 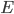$E$ is connected on the plugboard. We can now deduce for all the letters in the cycle to what letter they’re connected on the plugboard. Now we can also deduce to what letter 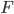$F$ is connected on the plugboard, and in particular, we can deduce again to what letter $G$ is connected, as a sort of check.

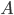It turns out that, more often than not, this gives a contradiction in the plugboard settings, like a letter that is connected to two letters at the same time, which is not possible. This means we have found a contradiction in our original hypothesis, which means $G$ is not connected to $A$ on the plugboard.

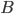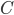Now we can test another hypothesis, for example: $G$ is connected to $B$ on the plugboard. After that, we may test the hypothesis that $G$ is connected to $C$ and so on. Most of these hypotheses will end up in a contradiction, but some may seem valid. This does not necessarily mean we have found the right plugboard setting, since we also guessed the rest of the Enigma settings at the start of the process. This means we also have to check all possible settings, which may take quite some time by hand.