Around the world, tens of thousands of people are waiting to receive a kidney transplant. Read how mathematics can help more people receive one.
Kidney exchange
For 2020, Eurotransplant, the transplant organization of which The Netherlands are a part, reported over 5600 new registrations on their waiting list, these are patients in need of a kidney. On the other side of the ledger, only about 2800 deceased donor transplants were performed (Cite ET annual report). Living donation makes up part of this shortfall. Since a single kidney is sufficient for a healthy life, family or friends sometimes offer one of their kidneys for transplant.
A major hurdle for kidney transplant is the compatibility of donor and recipient. Besides the well-known blood group requirements for transplantation, many other factors may make a particular transplant too risky. Of particular concern are the human leukocyte antigens (HLA) of patient and donor. If the HLA profiles differ, the recipient’s immunological system can produce antibodies, possibly leading to rejection of the transplanted kidney. These antibodies stay around and can also be created through other sensitizing events such as pregnancy and blood transfusion. Transplants from a donor with HLA against which the recipient already has antibodies are substantially more risky. For these reasons, not every donor can donate to any recipient, and some patients who have found a willing living donor are still unable to receive a transplant.
Kidney exchange offers a solution to this problem. The basic idea is simple, consider two recipient-donor pairs. In both pairs, the donor is willing to donate to the recipient, but is incompatible. In pair 1, the recipient has blood type A and the donor blood type B. In the second pair, the roles are reversed with a blood type B recipient, and a blood type A donor. The donors can now be exchanged between the pairs. The donor of the first pair donates to the recipient of the second. In return, their friend or family member receives a donation from the second donor.
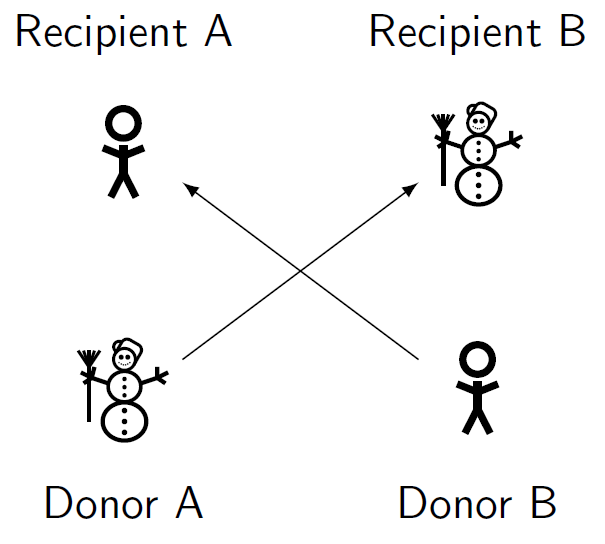
Figure 1: A simple kidney exchange. The donor of each pair donates to the compatible recipient in the other pair. This is called a two-way exchange, as it consists of 2 recipient-donor pairs.
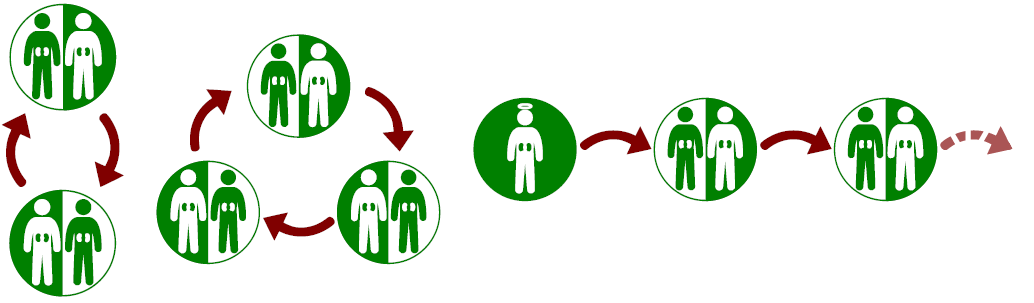
From this simple idea, kidney exchanges were born. Moving beyond ad-hoc matches of pairs, transplant centres and national health organizations started combining information of large pools of donor-recipient pairs, increasing the number of possible transplants identified. New modes of transplant were introduced. Within the larger pools, longer cycles can be identified. Non-directed donors, who do not have a specific recipient they wish to help, allow for chains of transplants. As there is no need for a specific recipient to receive a transplant in return, these can theoretically go on forever.
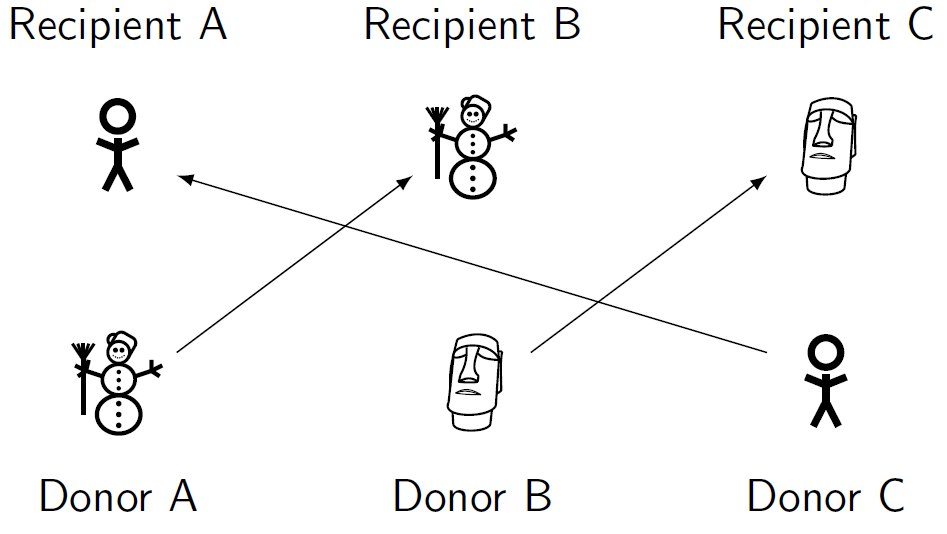
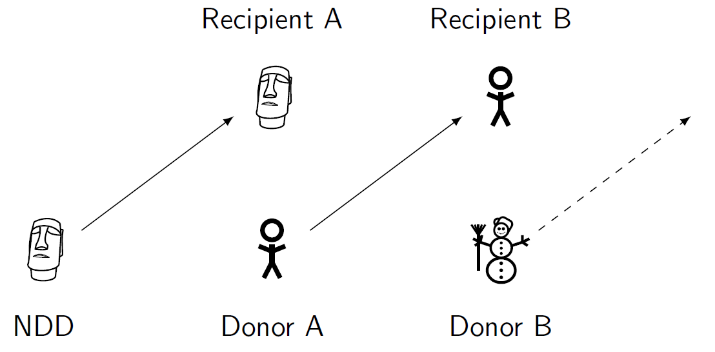
Figure 2: On the left, a three-way exchange. On the right, a chain of transplants. Donor B might provide a transplant to another recipient at a later date.
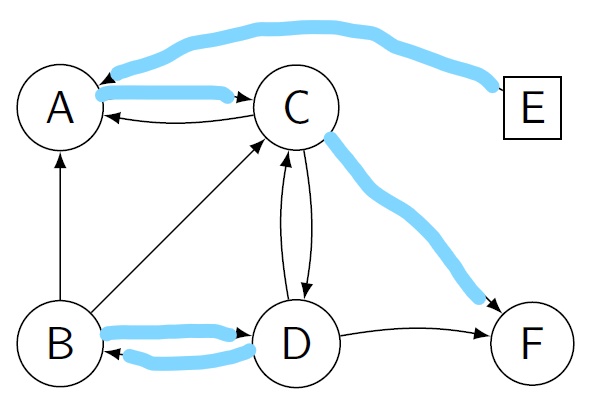
Kidney exchanges are by now well established. In the UK, the largest European programme, over 300 pairs participate in the quarterly matching runs, leading to about 200 transplants per year. The Netherlands hosts the oldest European national kidney exchange, with around 50 participating pairs per matching run, enabling 22 transplants in 2019. A small-scale version of the problem they face is illustrated in the figure below.
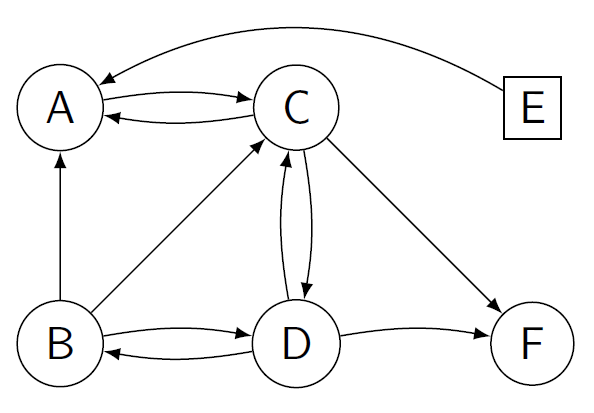
Figure 3: In this figure a single circle represents a recipient-donor pair, while a square represents a non-directed donor. Arrows between nodes mean that the donor at the start of the arrow can donate to the recipient at its end. The goal is to find cycles and chains in such a graph maximizing the total number of transplants.
A puzzle to think about In the figure above can you think of a scheme such that all recipients receive a transplant?
Due to the size of these exchanges, a powerful mathematica method called integer programming is employed to identify the best possible combinations of transplants. The objective is generally to maximize the number of transplants in a solution, alongside tie-break criteria. This objective must be maximized under the constraints that every chosen transplant is part of a valid cycle or chain, and that each recipient or donor is only transplanted once.
Handling uncertainty in kidney exchange
Kidney exchanges are plagued by uncertainty. During a matching run, all known incompatibilities between recipients and donors are taken into account. However, it is common that potential transplants in a proposed solution turn out to be incompatible after further testing. On top of this, donors and recipients can drop out of the programme between a matching run and the actual transplant for a variety of reasons. Compounding the issue, cancelling transplants forces the complete transplant cycle to be cancelled, as taking out even one transplant means there is no more equal exchange between all pairs. Likewise, a transplant cancellation means cancelling the downstream portion of a transplant chain. Transplant cancellations are common in practice, in the UK, only 60 to 70% of proposed transplant proceeded.
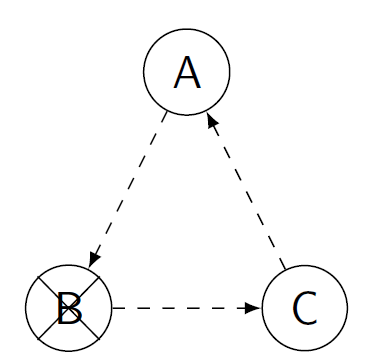
Figure 4: In these images, a single circle represents a recipient-donor pair, while a square represents a non-directed donor. In both images, pair B drops out. On the left, this cancels the whole cycle, as C will no longer participate if the pair does not receive a kidney from B. On the right, the transplant to pair A can still proceed, but no other transplants can be performed.
Kidney exchange programmes have implemented various policies to reduce the impact of transplant cancellations. The Netherlands makes use of a central reference laboratory for compatibility testing. Proposed transplant plans can be checked quickly for compatibility and completely changed if necessary, ensuring the final proposal only includes compatible transplants. Such centralized labs allowing for quick testing are rare, and easier to organize in smaller countries. The UK therefore computes solutions where as many transplants as possible are contained in two-way exchanges, to make sure cancellations have limited impact. Furthermore, when using three-way exchanges, they prefer those with an “embedded” two-way exchange, which provides a back-up solution in case a transplant involving the third pair becomes impossible.
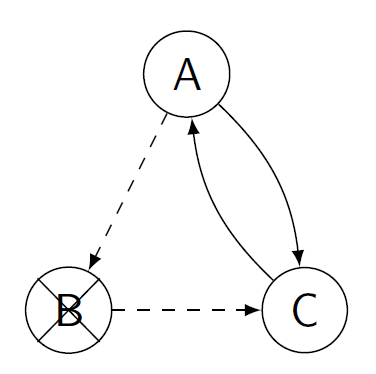
Figure 5: A planned three way exchange with pairs A, B and C. Donor B could also donate to recipient A. If pair C drops out, the “embedded” exchange between A and B can be performed instead.
Mathematical Optimization
The problem of protecting kidney exchanges from uncertainty has inspired researchers to investigate more recourse strategies for planning transplants. As with the UK’s “embedded” strategy, these consist of a main proposed solution, but they also call for testing additional potential transplants. These extra tests provide back-up options, allowing the solution to be changed in case the main solution turns out to be impossible.
Constrained recourse strategies limit back-up options to particular configurations. The back-up options must have a specific relation to the “main” solution. Embedded strategies are one example, where the back-up options are only allowed to be potential transplants between pairs in the same “main” cycle. Another example are subset recourse strategies, which divide the pool into small subsets and test all potential transplants within them, but do not allow testing of transplants from one subset to the other. Such simple testing strategies can still improve the expected number of transplants compared to strategies used in practice. In particular, testing short overlapping cycles, as illustrated below, appears promising.
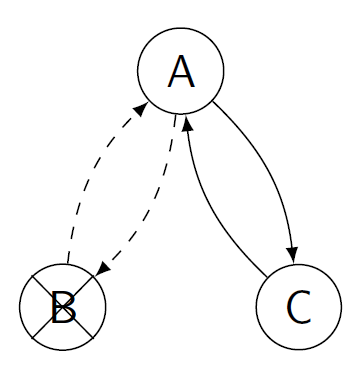
Figure 6: The cycle between pairs A and B is the first option, but in case pair B drops out, the overlapping cycle between A and C serves as a back-up option.
More complex strategies, where testing potential transplants is only limited by testing capacity in the labs, are also being studied. Computing optimal strategies for this lightly constrained case is challenging. Despite use of advanced optimization techniques, current algorithms can’t yet scale to the size required for large real-life kidney exchanges. However, testing plans found by these strategies for small and medium sized recipient-donor pools confirm the power of overlapping cycles, and show promise that further gains in the expected number of transplants can be made.
A second avenue of research is into worst-case scenarios. Instead of choosing tests to maximize the expected number of transplants, the goal now becomes to maximize the number of transplants if a fixed number of transplants fail. However, these failures occur exactly where they most disrupt the solution. Computing optimal solutions in this setting is something of a cat-and-mouse game. Since the number of possible combinations in which transplants can fail is too large to take all of them into account, only a small number are used initially. Any proposed solution is then stress-tested, the most disruptive failure is computed to see if it is worse than those already considered. After a back-and-forth of new proposed solutions, and new failures maximally disrupting these, a solution will be found that maximizes the number of transplants given worst-case failures. Strategies guarding against worst-case failures are in practice easier to compute for realistically sized kidney exchanges, and a sensible objective for the risk-averse, explaining their popularity in kidney exchange.
Due to their practical relevance, and clean mathematical properties, kidney exchange has become a popular subject in mathematical optimization. Through cooperations between organizations running the kidney exchanges and academia, advanced optimization techniques have found their way to practice, an important contribution that continues to grow as kidney exchanges become larger and more complex.
Interesting reading
If you are interested in learning more about Kidney Exchange in practice, particularly in Europe, I recommend the following papers.
Biro et al. Building Kidney Exchange Programmes in Europe—An Overview of Exchange Practice and Activities, Transplantation, 2019, p 1514-1522.
Biro et al. Modelling and optimisation in European Kidney Exchange Programmes, European Journal of Operational Research, 2020.
References
Eurotransplant Annual Report 2020.
NHS Blood and Transplant - Living Donor Kidney Transplantation Overview of Activity and Performance.
Back in 2015, I joined the Movember health movement, a movement that you probably have heard of having something related to men growing a moustache. As a woman, you might imagine, I did not join for the moustache thing, but rather for the cause behind the moustache symbol, that is, raising awareness of prostate and testicular cancer.
After a busy week at work, Reinforcement Learning slowly sinks into his leather armchair. A smoky aroma fills the room to the tune of a crackling fire. With a deep gaze fixed on the flames dancing in the fireplace, he leisurely takes a sip of red wine.
Phenomena like social cohesion and polarisation emerge from individual interactions on the social network of relationships between people. So, what does this network look like?
How can one hope to understand the precise structure of a virus if it is able to become unrecognizable within weeks? The mathematics behind this questions didn't let go of my mind for extensive periods of time during my PhD studies in Belgium.
