We need natural numbers to count the days, rational numbers to measure the portions of cake we have eaten, real numbers to weigh groceries, and complex numbers to describe the physics of the tiny particles.
It is undeniable that natural, integer, rational and real numbers are necessary to explain what happens in our daily life, but in high school some of us also hear about some weird objects called imaginary numbers, also known as complex numbers.
During our teen years, teachers repeated thousand times that the square of every real number is a non-negative number. They also insisted that this golden rule implies that some polynomial equations, such as 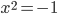, have no real solution. This lack of appropriate objects to solve something as simple as 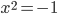worried mathematicians for a long time. Thus, in the 16th century they invented the imaginary unit, 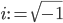, that satisfies the desired identity 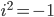. 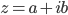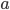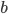This gave birth to the complex numbers, which are those that can be written as , where and are real numbers. Nevertheless, the complex solutions to polynomial equations do not model any physical reality at first glance, and that is why they were baptized as imaginary numbers.
However, complex numbers became useful in a few fields of physics, such as optics, electromagnetism or quantum mechanics. In the case of optics and electromagnetism they only simplify notation.
On the other hand, quantum mechanics, the branch of physics that explains the behavior of tiny particles, is the only well-established theory describing nature whose rules (postulates) are written in terms of complex numbers. It was developed in the early decades of the 20th century and is one of the most accurate physical theories nowadays.
Nonetheless, it is not clear that imaginary numbers should necessarily appear in the foundations of this theory. The reason is simple: everything that we can measure in nature can be quantified with real numbers. This was something that made Schrödinger and Lorentz, two of the founders of the field, feel uneasy:
What is unpleasant here, and indeed directly to be objected to, is the use of complex numbers. We should be able to only use real numbers.
We read this in a letter from Schrödinger to Lorentz, June 6th, 1926. The exact quote is slightly more technical:
What is unpleasant here, and indeed directly to be objected to, is the use of complex numbers. 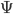is surely fundamentally a real function.
We simplified the sentence without changing the essence for the sake of understanding. And it turns out that they were wrong: complex numbers are unavoidable in quantum mechanics.
On the one hand, many attempts have been made to delete complex numbers from the rules of quantum mechanics, but none of them has been utterly satisfactory. On the other hand, quite a lot of physicists have proposed theoretical ways of showing the inevitability of complex numbers, but most of them do not provide a way of testing in practice their theoretical predictions.
It was not until 2021 when an experiment to prove the necessity of complex numbers was proposed by Renou, Trillo, Weilenmann et al.. So far this experiment has not been fully realized and we may have to wait a few years until it is done. Manipulating quantum systems is one of the biggest challenges for engineers nowadays, as it, for instance, requires controlling particles that are at -270°C. However, this is a breakthrough that will probably confirm that imaginary numbers are a reality.
The experiment proposed involves non-local games, which were used by Bell in 1964 to suggest a way to refute Einstein’s opinion that quantum entanglement can be explained by classical physics. In fact, this year’s Nobel Prize in Physics was awarded to Aspect, Clauser and Zeilinger for experimentally realizing Bell’s proposal to show that quantum entanglement cannot be explained by classical physics.
Entanglement is one of the amazing features that characterize quantum mechanics. One way of visualizing its power is through the following example. Consider two experimentalists, Alice and Bob, that gather together in a lab and prepare two tiny particles that are entangled. After that, they take one particle each and travel to two very far away locations. Say the Moon and Mars, respectively. When Alice is at the Moon, she paints her particle with a green or red pen. The surprising consequence is that Bob’s particle instantly gets colored by green or red, respectively. This way, thanks to entanglement, Alice could affect not only her local environment, but also Bob’s particle, despite the long distance. This non-local effect is intrinsically quantum, and non-local games were baptized like that because they allow to certify this quantum behavior. Similarly, Renou, Trillo, Weilenmann et al. proposed a non-local game that allows to certify the need of complex numbers.
Their game has three-players (Alice, Bob and Charlie) and one referee (Roman). A round of the game consists of Roman sending a trio of questions, one to each of the players, and then Alice, Bob and Charlie, answer back to Roman. The players win if the joint answer is the correct one. The probability of the referee asking any trio of questions and which are the correct answers to each trio of questions are publicly known. However, Alice, Bob and Charlie are far away from each other, and thus they cannot communicate during the game, so once they receive a question they cannot know which questions have been sent to the other players. What they can do is talk before playing and agree on a strategy. They can even share quantum entangled particles that allow them to access non-local effects.
To imagine a round of the game, we introduce a concrete example (illustrated in the picture below). Say that there are two possible trios of questions are (RED, GREEN, RED) and (BLUE, RED, RED), which both are asked with probability 0.5 and whose respective correct answers are (LION, ZEBRA, ZEBRA) and (ZEBRA, LION, TIGER). In this case, Charlie is always going to receive question RED, but to win he should answer differently depending on which are the questions asked to Alice and Bob. This way, if they share no quantum entanglement, they cannot win with certainty, as the players cannot communicate and cannot act non-locally. However, if they share quantum entanglement they can always win, because they can act non-locally and Charlie can know which questions were asked to Alice and Bob without communicating with them.
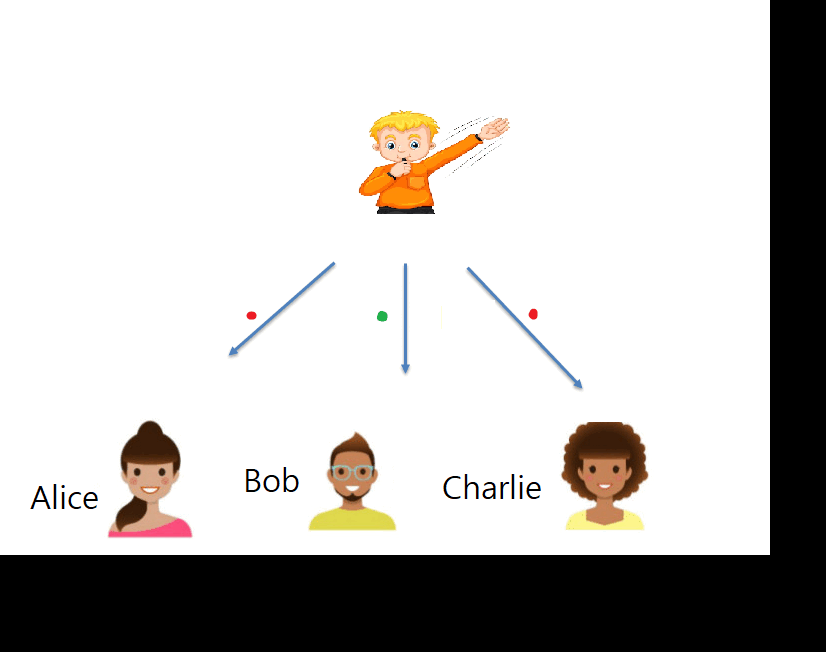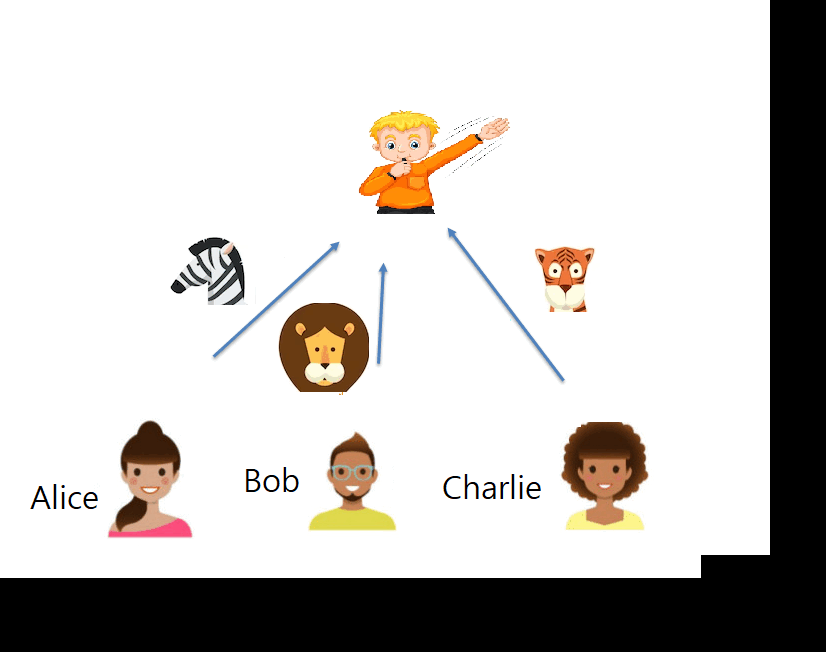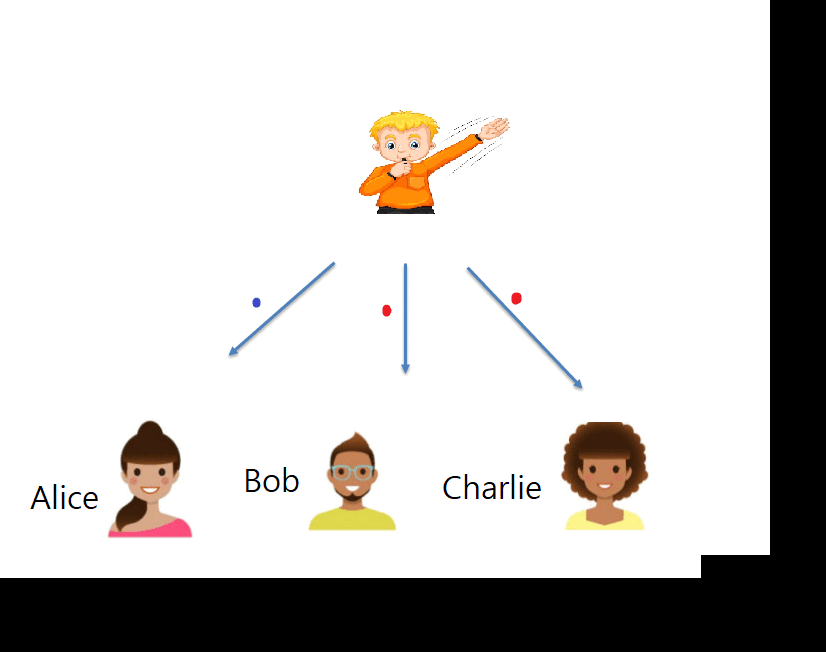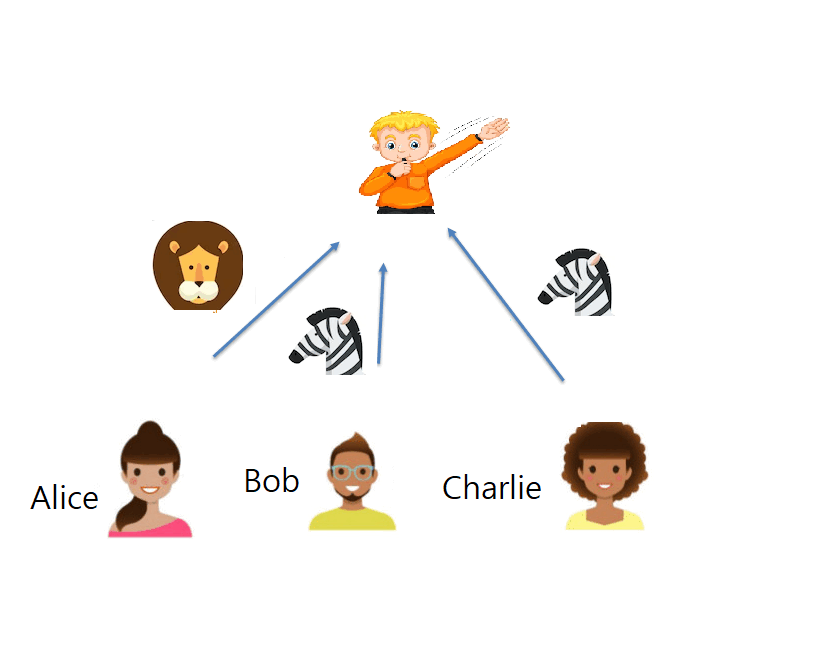
The simple game that we described above can be won with both, quantum strategies described by real numbers and quantum mechanics described with complex numbers, so it does not work to separate both theories. The game proposed by Renou, Trillo, Weilenmann et al. is more elaborated. In particular, they do not allow entangled particles to be shared between Alice and Charlie, only between Alice and Bob, and Bob and Charlie. That constraint is essential in their theoretical proof of the fact that quantum mechanics with complex numbers outperforms quantum mechanics with real numbers when playing this game. This result leads to a natural route to confirm that imaginary numbers exist in reality: play this game in three incommunicated laboratories and show that you can outperform the theoretical upper limit to the performance of real numbers. If that is done, then it would be evidence that something far from real numbers is needed to explain quantum mechanics, making complex numbers inevitable.
Imaginary numbers were born as abstract mathematical entities, then they became useful in physics, and apparently fundamental in quantum mechanics. Despite the fact that their essential role in quantum mechanics had been questioned, recently an experiment was proposed to certify their necessity in the description of quantum mechanics. This way, imaginary numbers do not seem to be a whim of mathematicians. If they had not introduced them, physicists should have done it to explain the behavior of the tiny.
The story goes as follows, during the last couple of decades many scientists, universities, and tech giants like IBM, Microsoft, and Google have invested largely in building this advanced machine called a quantum computer. Such a computer will be able to perform quantum computations, which rely on qubits instead of ordinary bits. The major challenge when you want to use such a qubit is that it is very unstable, and stable qubits are essential to have a proper quantum computer.
During the last decades, many resources have been invested in quantum computing. This research field has grown immensely and amazing results have been obtained. The plans for the future are highly ambitious, but at the same time, there are serious questions that need to be addressed.
With ever-growing possibilities and interconnectivity on the internet, we rely more and more on it being secure. However, our classical internet is not provably secure, could a quantum internet solve our problems?
QuTech at the Delft University of Technology and TNO, in collaboration with the European Quantum Internet Alliance, are leading the efforts to establish a quantum Internet and aims at having a proof of concept version, between the cities of Amsterdam, Leiden, Delft and the Hague.
Have you ever wondered what kind of insights you can gain about games by looking at it using a mathematical lens? In this article we have a look at Snakes and Ladders, and in a follow up article we will dive into Monopoly!
, have no real solution. This lack of appropriate objects to solve something as simple as 
, that satisfies the desired identity 
. This gave birth to the complex numbers, which are those that can be written as 
, where 
and 
are real numbers. Nevertheless, the complex solutions to polynomial equations do not model any physical reality at first glance, and that is why they were baptized as imaginary numbers.
is surely fundamentally a real function.
