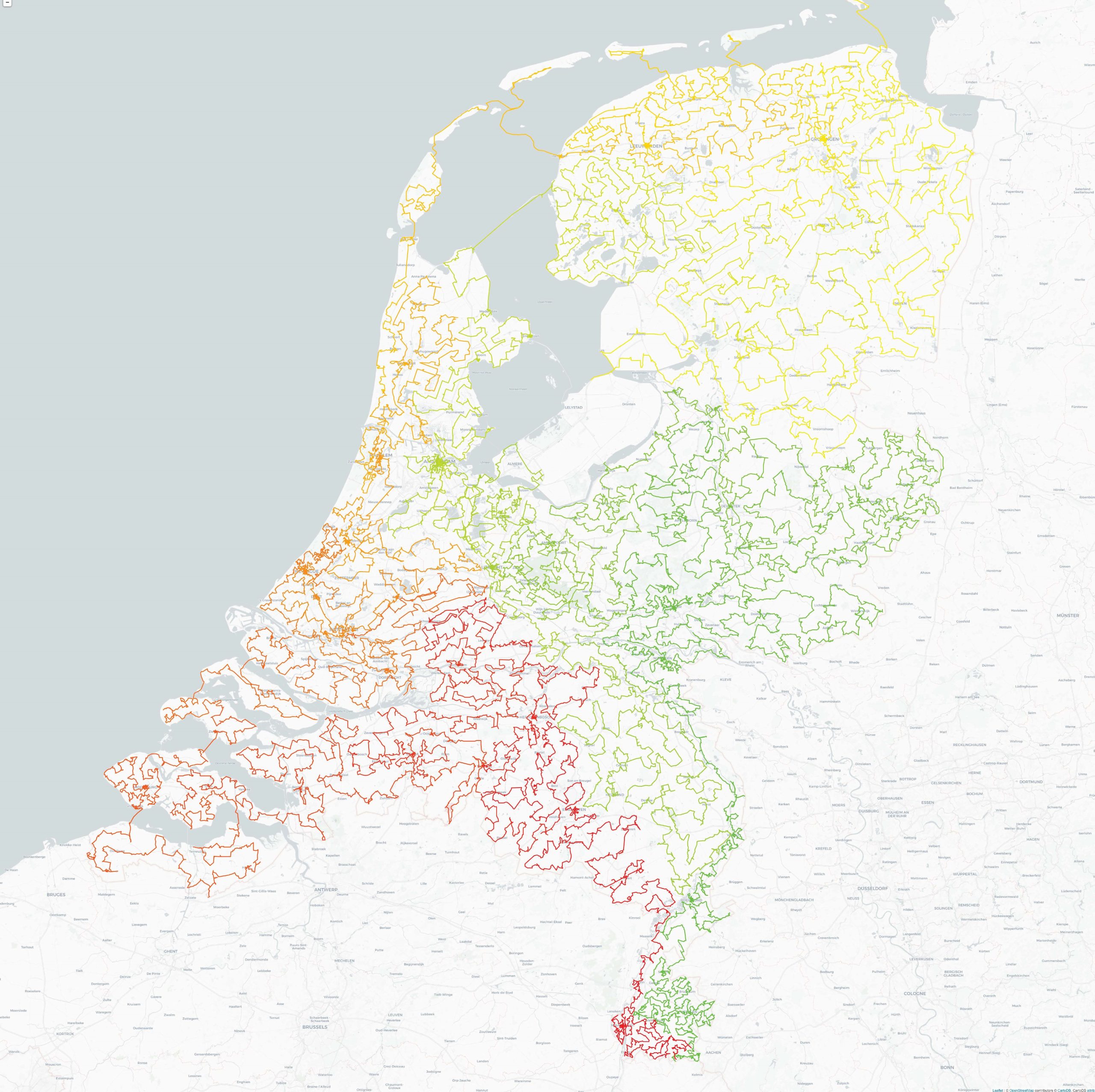
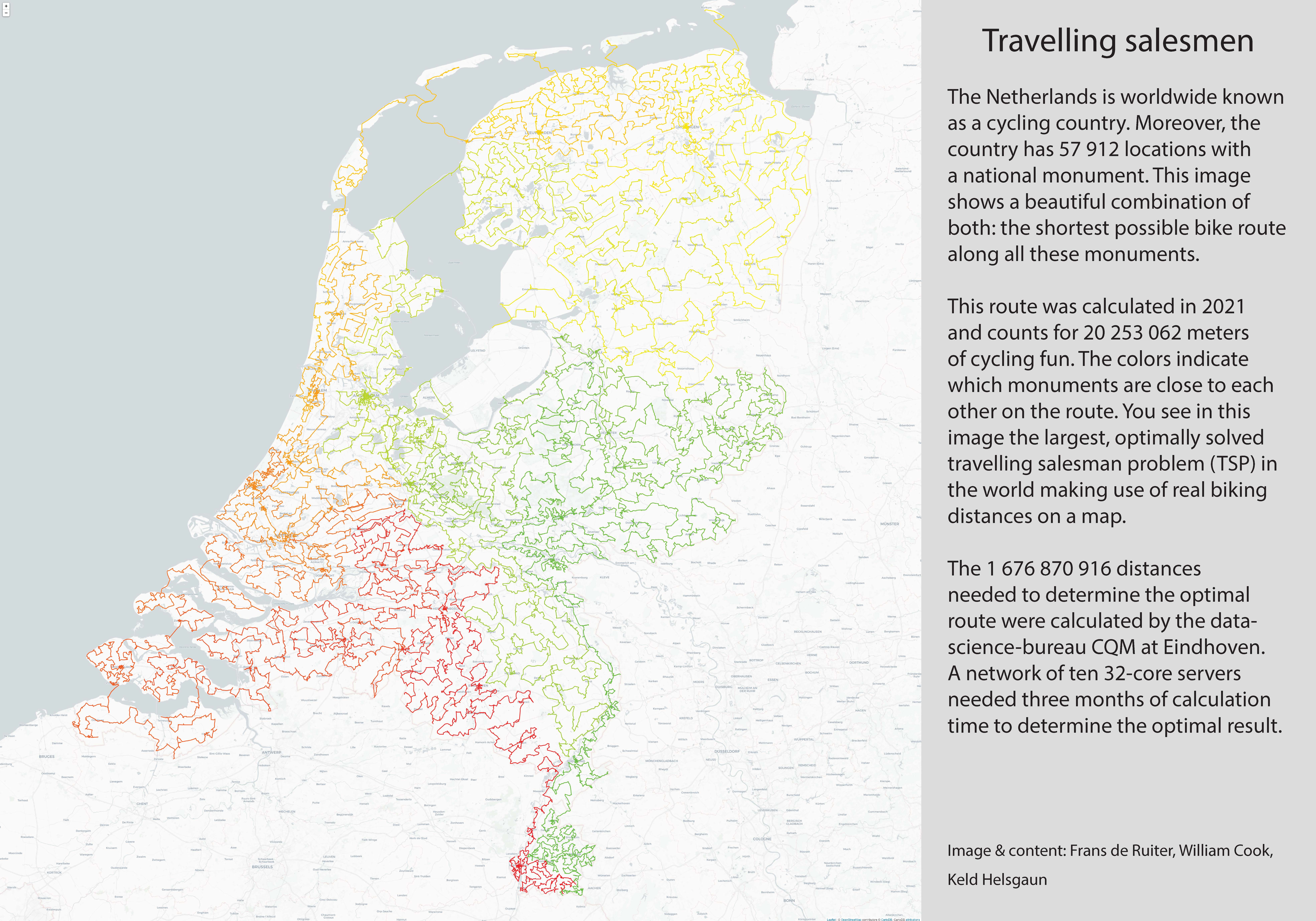
Below a poster about The travelling salesman problemwhich was made for mathematics exhibition IMAGINARY. This poster was made by Frans de Ruiter from the Dutch company CQM
Poster created by Frans de Ruiter, in collaboration with the Network Pages.
The traveling salesman problem
Suppose you have a delivery service. You have one truck and have to deliver a large number of parcels to different cities in the country every day. Then you run into the following problem: in which order should you visit the cities? In other words, you want to find a tour that starts at the depot where the packages are kept, then visits each of the given cities, and finally returns to the depot. The goal, of course, is to find a tour with minimal travel costs. Here, travel costs can refer to the average time it takes to complete the tour or the total length of the tour.
Computer scientists call this problem the traveling salesman problem or TSP for short. You may think that if we know the cities to visit and the travel costs of the roads they connect, a computer can easily find the shortest tour. But the fact that TSP is so easy to claim is deceptive: using strong algorithms the shortest tour can be approached very accurately and fast, but proving that, given the distances, there cannot be a tour that is even an inch shorter is extremely difficult. The Traveling Salesman Problem has become so popular that it even has its own website, with applications ranging from finding the optimal pub crawl in the UK, to determining the optimal interstellar journey between stars! For example, this poster shows the optimal tour between 57,912 national monuments in the Netherlands!
Can you imagine that the TSP is one of the most challenging problems in theoretical computer science? Do you want to know why? And would you like to read about recent breakthroughs in the TSP? You can view this article for more information on the result shown in the poster, this article to get a taste of the research mathematicians do on the Traveling Salesman Problem, and this website for much more information on this problem.
Feel free to print and use this poster for educational purposes. Since this material is protected under a Creative Commons licence we ask you to mention Anna Priante and the Network Pages when using it.
Recently there has been a breakthrough in the field of algorithms for geometric network problems, concerning the complexity of the Euclidean Travelling Salesman Problem.
Are you one of those people who always seems to pack just a bit too much for your car to handle when packing for a vacation? Then you should have a look at this article!
