When thinking about social networks, we all have examples that come to mind: Facebook, Twitter, TikTok, but also Snapchat, WhatsApp, or LinkedIn. In general, anything composed of relations between individuals can be seen as a social network and studied as such. However, as individual members of these networks, we might often feel like a grain of sand in that vast desert of people.
What can a single grain of sand understand about the vastness of the desert? What can the single social network user we are extract from these multi-billions entities we belong to?
Using three popular TV shows, we will see that there is a lot more to be said about the global structure of a social network from our local perspective as users.
Fans and characters of Game of Thrones
If you are a Game of Thrones fan, you likely remember that episode in which we all learned who the actual parents of Jon Snow were. In just one flashback from his younger brother, he became a major force to reckon with in the chase of the ultimate power: sitting on the Iron Throne. At this moment, we all knew that this news would change the dynamic of the story and we could not wait to see this information reach his ears. It took a whole season and a reunification with his dear friend Sam for him to finally learn the truth about his parents.
This example perfectly highlights the contract between local and global. On one hand, we, the audience, have access to the global information: we see the point of view of diverse characters, get to hear private conversations, and know about events exactly when they occur. On the other hand, the characters only have access to local information: they experience their own story, mostly discuss with relatives or friends, and hear about far away events later on, if ever.
This contrast naturally raises the question of what kind of global information is locally available? And the answer is, a lot more than expected! To understand this let us focus on a network perspective.
Consider the main characters in Game of Thrones and connect them if they are siblings, married, or close friends. This leads to the network below. Now, what does local and global mean here?
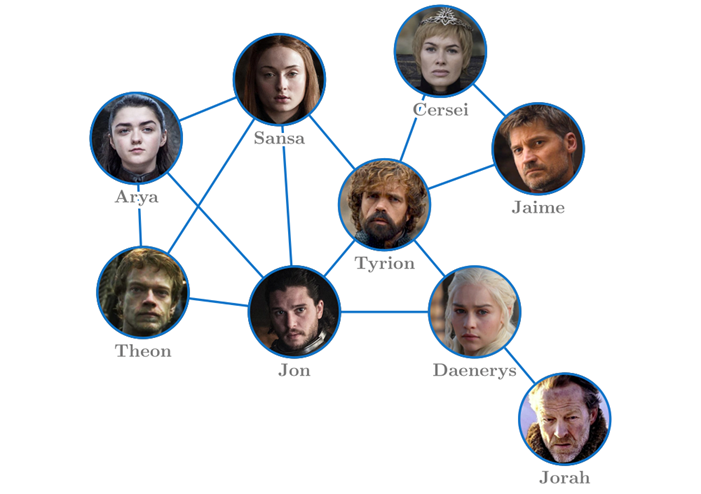
Imagine seeing the world from Jon’s perspective. You are in contact with five persons: Sansa, Arya, Theon, Tyrion, and Daenerys. By discussing with them, you could further get to see their inner-relationships, like the fact that Sansa, Arya, and Theon form a triangle of connections and that Tyrion and Daenerys know each other. Finally, you could ask them to describe their own perspective in a similar way you just did and discover that Tyrion is connected to two persons you did not know: Cersei and Jaime. This corresponds to the local information of a network: what a single member can infer from asking their friends questions (these friends can also further ask questions to their own friends, etc).
Consider now your perspective as a spectator of the TV show. Not only do you get to see the previous network from a global perspective and can draw it, but you also get extra information about relationships between characters. For example, it is not difficult to see three groups in this network: the Stark family (Arya, Sansa, Jon, and Theon), the Lannyster family (Cersei, Jaime, and Tyrion), and Daenerys with Jorah. And this makes sense with regards to the story of the show! Similarly, we can see that Tyrion seems to be a particularly central member of this network, which also arises from the plotline: he is a Lannyster, married to Sansa, and allied with Daenerys and Jon. This corresponds to the global information of a network: what can only be seen when taking a step back (such as communities like the families, or hubs like Tyrion).
Using the contrast between a single character’s perspective and our global view of the network, we will see how local and global properties interact with each other using two interesting results: the friendship paradox and the number of communities.
Popularity contest in Friends
Put now your shoes into Phoebe Buffay’s for a second. You are obviously the coolest woman on earth. You are a survivor, an artist, a sparkle of joy. You are the best person there is, but, somehow, you do not feel like the most popular within your own group of friends. Think about it: you mostly live alone when everyone has nice roommates, the love of your life lives in Minsk when everyone gets married, and even your family is a mess when everyone else has fun siblings and parents. This does not make sense! Why do you feel so left out? Is that a normal feeling? Well, the answer is yes, and you are actually not the only one there!
Phoebe’s feelings arise from an interesting property of networks: the friendship paradox. Let us now see what this paradox is saying and why it arises from a contrast between local and global properties in a network. Consider the six main characters of Friends and connect them if they are either siblings, married, or roommates. The leads to the network below.
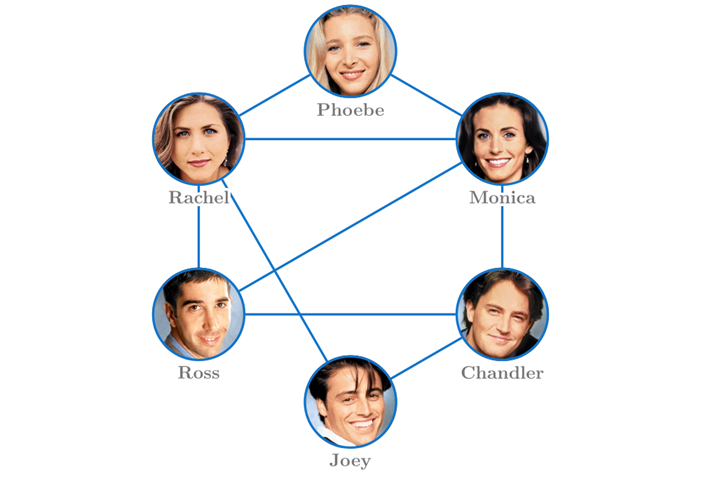
Imagine picking a person from this group of six at random and counting their number of connections. On average this person would have 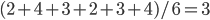connections. Now, in a similar manner, imagine picking the friend of a person at random and counting their number of connections. This changes a bit the odds of picking every individual person. For example Phoebe was chosen with probability 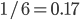before, but now with probability 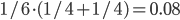(first pick Rachel or Monica and then Phoebe among their 4 connections). Similarly, Rachel was chosen with probability 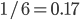before, and now with probability 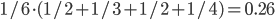(first pick Phoebe, Ross, Joey, or Monica and then, for each of them, choose the connection towards Rachel). By doing this for all 6 characters, we get that, on average, the friend of a person has 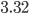connections!
Where does this difference come from? The answer lies within the friendship paradox!
The friendship paradox states that a randomly chosen person in a network is likely to have less friends that one of their friends chosen at random. This arises from the fact that very popular people will, by definition, have lots of friends and thus are likely to be picked as the friend of someone. This is particularly obvious when considering the change of probability to pick Phoebe or Rachel between the first and the second experiments: while both are 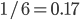in the first experiment, Phoebe’s drops to 0.08 in the second one while Rachel’s reaches a high 0.26!
What does this paradox have to do with local and global properties of a network you ask? As mentioned before, the number of friends of a person and the number of friends of their friends is a local property: it can be found by counting your friends and asking them to count their own friends. So the observation that your friends are more popular than you arises from local information. However, the fact that this is true comes from a global property, more specifically the fact that popular people have a global impact on the network. In other words, the friendship paradox can be interpretated as the fact that network hubs are connected to many persons and thus affect most local friend groups.
So now, next time you feel bad like Phoebe does, remember that you are actually the coolest person on earth who just got tricked by a mathematical paradox.
Departments in The Office
Another usual day in Scranton: the electric city slowly wakes up to the sun, the local Dunder Mifflin office sees his first workers arrive, and soon Michael Scott, the best manager ever, will arrive to start his day of work. However, and as per usual you might say, Michael is not in a working mood today. He would actually rather just spend time with his best friends, who all happen to work in the same office as he does! But today Michael has a special task from headquarters: to report how many departments he has in his branch. How can he even know that? People seem to be working and the branch is selling a lot of paper, so why is it his job to know what people are actually doing, right? And the headquarters keep asking the same question every year, so annoying… except that, this time, he has an idea: he will use their request as an excuse to discuss with everybody and will ask them a simple question: how many other persons are in your department?
Of all the questions to ask, this one feels too simple to be able to count the number of departments. Why not just ask someone if they already know how many departments there are? Or at least what department they belong to? Or even who they are working with? All these questions would give a lot more information and would easily allow him to count the number of departments! But no, he had to just ask everyone the number of other persons in their department. You cannot even distinguish two departments of the same size this way!
Luckily for us, this simplistic question can actually solve Michael's problem and will allow us to see the relation between local and global properties of a network. To do so, let us first consider the network of the office, where people of the same department are connected to each other.
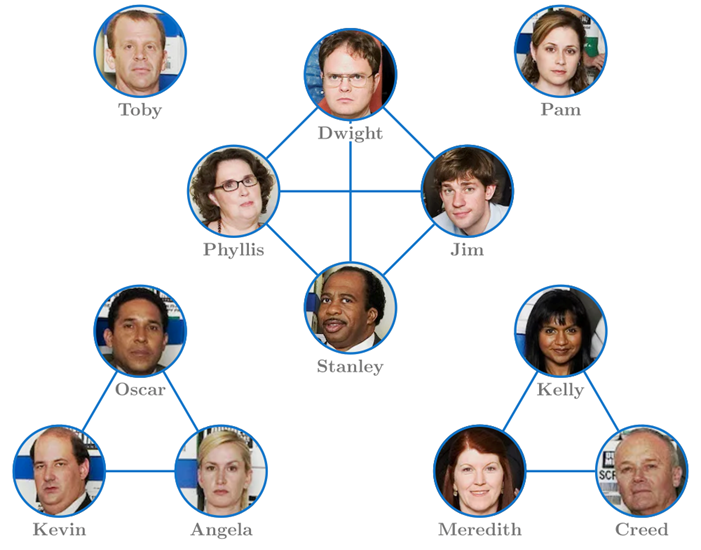
Considering the above network as a whole, we can see that there are 5 departments: Sales (Dwight, Phyllis, Stanley, and Jim), Accounting (Oscar, Kevin, and Angela), Support (Kelly, Meredith, and Creed), Human Resources (Toby), and Reception (Pam). Moreover, by asking everyone (for example in alphabetical order) the number of persons in their department, we would get: 2, 2, 3, 3, 2, 2, 2, 2, 0, 3, 3, 0. Imagine now for a second only getting the latter sequence of numbers. Can you deduct the number of departments from this sequence? The answer is yes!
There is a general formula for this problem, but the idea is that, every group of 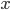persons mentioning that they work with 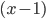other persons forms a department. For example, there are 4 people working with 3 other persons, thus creating one department of 4 workers. Similarly, there are 2 groups of 3 people working with 2 other persons, thus creating 2 departments of 3 workers.
Now, why does this come from a contrast between local and global? The number of departments here, or in general the number of communities within a network, is a purely global property: you need to see the whole network to be able to count them. However, we managed here to obtain this number by simply asking everyone something about their local information: the number of persons they work with within their department. So local information was able to make us deduce a global property!
This computation shows once again that the laziness of Michael Scott can be saved by one of his coworkers, one with enough mathematical knowledge in this case.
The desert is not so vast
The relation between local and global in a network is not limited to the two properties presented here and include a wide and surprising class of results with active research in the area. Thus, next time you feel like that lost grain of sand in the social network desert, remember that a lot more can be seen from your perspective and a single blow of wind might suffice to find that oasis you were looking for.
A conjecture of Erdős and Hajnal from 1989 says that forbidding any specific substructure results in existence of a very large homogeneous one! In this article you will have a look into one of the most fascinating problems in modern graph theory.
An echo chamber is a community wherein the same opinions are bounced around, endlessly ‘echoing’ with barely any change. And as they do, any other opinion is shunned, pushed aside, and eventually just rejected without consideration.
Since 2016 the world has been witnessing the Rohingya genocide in Myanmar, in 2021 we all saw the Capitol riots on tv. What do networks have to do with these events?
How can one hope to understand the precise structure of a virus if it is able to become unrecognizable within weeks? The mathematics behind this questions didn't let go of my mind for extensive periods of time during my PhD studies in Belgium.
Common sense tells us that objects of comparable size should be equally hard to find. Yet, when searching inside a random network, surprises are awaiting . . .
connections. Now, in a similar manner, imagine picking the friend of a person at random and counting their number of connections. This changes a bit the odds of picking every individual person. For example Phoebe was chosen with probability 
before, but now with probability 
(first pick Rachel or Monica and then Phoebe among their 4 connections). Similarly, Rachel was chosen with probability 
(first pick Phoebe, Ross, Joey, or Monica and then, for each of them, choose the connection towards Rachel). By doing this for all 6 characters, we get that, on average, the friend of a person has 
connections!
persons mentioning that they work with 
other persons forms a department. For example, there are 4 people working with 3 other persons, thus creating one department of 4 workers. Similarly, there are 2 groups of 3 people working with 2 other persons, thus creating 2 departments of 3 workers.
