On Wednesday I was teaching an exercise class on graph theory. There was this one exercise that was troubling me for a couple of days, I couldn't solve it and it was frustrating.
Half an hour before my class I was sitting and thinking about it, and then I got the idea of the solution. I knew this was the correct idea. I was looking forward to discussing it with the students, but when I wrote the solution on the board I realized that a final touch was missing from my proof! What do you do then as a teacher?
Before I continue with my story let me give you some context. Graph theory is one of my favourite subjects in mathematics. A lot of problems related to graphs look more like puzzles, and you often don't need prerequisite knowledge to start working on them. You can also make drawings of graphs to come up with ideas and answers.
At the same time, in graph theory, many results are seemingly simple to state, but proving them rigorously demands a lot of work. The class of this week was about colorings of graphs. This is a wonderful topic, that has raised many interesting and difficult questions that have bothered and may still be bothering many mathematicians.
As you can imagine, the problem I was thinking about until half an hour before class started, and wanted to show in the class, was about colorings.
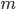To start with, what is a coloring of a graph? Say you have a graph with points and edges connecting some of the points. In a coloring the goal is to color all the points of the graph in such a way that no points that are connected with an edge have the same color. Of course, a trivial way to color the graph is by assigning to each point a different color and then you are done.
You can color this graph using four colors.
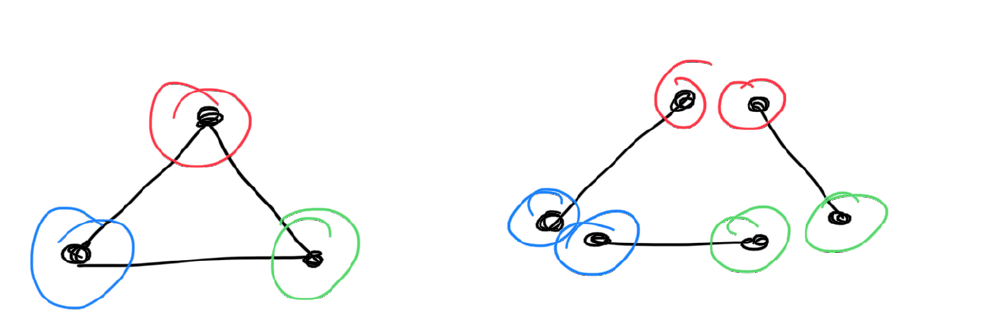
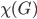It becomes more interesting when you ask what is the least number of colors that you need to color a graph so that no points that are connected have the same color. This number is called the chromatic number of the graph , and is denoted by . If we look at the graph shown above, what is its chromatic number? Can we color it with less than four colors? It can indeed be colored using three colors. How? Hence 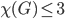. Can it also be colored using 2 colors? If not then we have shown that the chromatic number of this graph is 3. As an exercise, you can compute the coloring numbers of the following graphs.
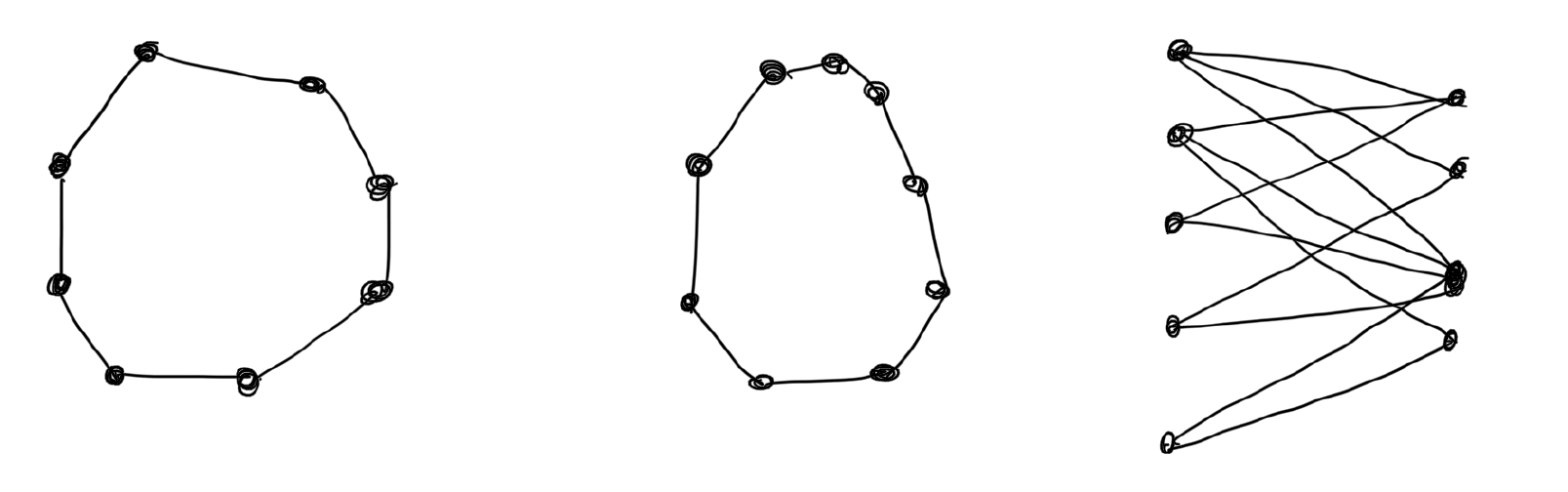
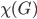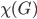Now we can discuss the exercise I wanted to show in class. Suppose that you have a graph with chromatic number . Suppose you color with colors. Take some line in the graph , and look at the colors of the two endpoints, then these will never be the same since this is not allowed in a coloring. We can see that each edge corresponds to a pair of colors, namely the colors of the two endpoints.
In a coloring each edge is assigned with a pair of colors.
The problem we had to solve is the following: show that if we color a graph with colors, all possible pairs of colors will be assigned to the endpoints of the edges. Translated into an inequality this can be written as follows. Show that
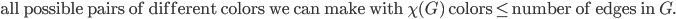
Or more compactly for the interested readers
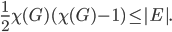
This is a wonderful statement I think, and it is not obvious why it should hold. There could be edges in the graph whose endpoints have the same colors, but why will there be no pair of colors that will not appear on some edge? This is what we wanted to prove in class!
The chromatic number of this graph is 3, and you see that all possible pairs of colors appear in the edges, (red, blue), (red, greed), and (blue, green).
You can assume that the inequality does not hold, then the reversed inequality should hold, which is
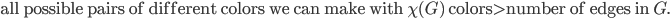
This means that there is a pair of colors, say (blue, green), that will not appear in any edge in the coloring. And this is where a very nice idea comes into play. If this happens then you can either remove blue or green from the coloring of the graph! Why? I will leave this puzzle to you, my dear reader.
Back to my initial question. I was discussing this problem with the students, and at some point I couldn't finish the argument. For a moment I stared at the board and then I could feel the silence in the room. Was it a good silence? Or an awkward silence? I don't know. I have no idea what everyone was thinking, but I wanted to avoid one thing, staring at the board for even longer, trying to come up with a solution which I would then serve to them, while creating this invisible wall between me and the students.
If you think about it, it is quite natural that this happens in class, when you do mathematics you get stuck (ok, it is not the purpose that this happens often, because it consumes a lot of time, and as a teacher, you also need to cover the material). But the students will have to go through this phase often in their future steps, teachers spend hours preparing everything and often make it look very simple. But it is not, when you do mathematics you get stuck, you need to find your way through it, and when you succeed it is a very joyful moment!
The silence should not be awkward, I think that the best thing to do is just start a group discussion, and try things out. Everyone should be engaged in the process of trying to find the solution, to experiment. The silence is good because it means everyone is thinking, while the awkwardness is not good, because then there are wrong expectations from both sides. I did my best to engage the students and ask their opinion.
I think that the discussion was very helpful because many questions and nice ideas were discussed. A curious thing with mathematics is that when you give the solution to a problem then it seems simple, and it makes sense, but it is not simple at all to come up with the solution yourself! You get stuck, and you need to think about it, but the solution is much nicer when you find it yourself than when someone shows it to you.
At some point, a student said "I found it!"; just to mention, we were already 40 minutes busy with this problem and we only had 5 minutes left, so I started feeling the pressure. When the student started explaining the solution I knew this was the missing part in the proof! I congratulated and thanked him, and wrote the solution on the board. This was a much nicer ending of the class than me explaining the solution! Now the solution was the result of a collective effort, and more people were involved in the process.
So what to do if something like this happens, just say you don't know it and engage with everyone to find the solution. When you do mathematics you will get stuck, the challenge is to accept this, learn to deal with this, and enjoy the process!
A mathematician once told me that problems that are very simple to state can be very deceiving, and sometimes turn out to be extremely difficult to solve. One such problem was the Four Color Problem.
Last week I had the honour to receive an award from the Amsterdam Young Academy (AYA) for my contributions in teaching in the BSc in mathematics at the University of Amsterdam. I thought of many things during this time, and I wanted to write some thoughts down.
A conjecture of Erdős and Hajnal from 1989 says that forbidding any specific substructure results in existence of a very large homogeneous one! In this article you will have a look into one of the most fascinating problems in modern graph theory.
I was very excited and interested when I heard some months ago about ChatGPT and what it can do. Both as a mathematician and as a teacher I was very curious about the responses it would give to my questions.
points and 
edges connecting some of the points. In a coloring the goal is to color all the points of the graph in such a way that no points that are connected with an edge have the same color. Of course, a trivial way to color the graph is by assigning to each point a different color and then you are done. 
, and is denoted by 
. If we look at the graph shown above, what is its chromatic number? Can we color it with less than four colors? It can indeed be colored using three colors. How? Hence 
. Can it also be colored using 2 colors? If not then we have shown that the chromatic number of this graph is 3. As an exercise, you can compute the coloring numbers of the following graphs.
