Think of a local car dealer selling cars in your region. To make sure new cars are delivered on time a whole mechanism involving various people, factories, and transport companies, must operate in coordination.
Raw materials need to be produced, gathered and sent to factories, where the various parts are manufactured. Think of tires, windshields, seats, or mechanical parts. Afterwards, all these parts are sent to a, possibly different, location where cars are assembled. The final step is to bring the new cars to the local dealers who will then forward them to the market. Have you even imagined that such a complex network of people and production steps must be coordinated for new products to reach the market? Both technological (telecommunications, the Internet, computer hardware and software) and mathematical advances (mathematical optimization, efficient algorithms, fundamental and applied research) have played a crucial role in making this possible. Let’s see how.
In general, similar background processes are related to many other products. Think of computers, TVs, smartphones, airplanes etc. The common factor is that many people and operations need to be timed and coordinated to guarantee that new products will arrive to the market on time. Furthermore, such production chains have changed in the past decades. Previously, it used to be that all parts were both manufactured and assembled into the final product at the same factory. But, in the past decades, companies no longer manufacture everything themselves, they rely on specialized factories for the various parts needed to construct the final product. And these specialized factories can be spread over the whole world. This whole chain of steps until the final product reaches the customers is called a logistics chain.
In recent years, the ”just-in-time” model has become increasingly popular for logistics chains. This model represents the desire to schedule everything in an optimal way. Advanced mathematical models and computer software have made it possible to find such mathematically optimal schedules. Such tools have had a huge impact on the global market since they allow companies to schedule their logistics chains with high accuracy. There is however a downside. If there is a disruption in one step, then probably there will be delays in the whole process, depending on the severity of the disruption. This happens, for example, when the stock of materials or time buffers are not large enough to respond to a disruption. We all remember what happened when the Suez Canal was blocked in March 2021 by the Ever Given, a huge 400m-long container ship traveling from China to Rotterdam. This incident had a global impact, many other ships couldn’t pass the canal, had to stay still for many days or find an alternative route, and oil prices started climbing.
In our recent research, published in Nature Physics, we did a more detailed and careful analysis of these mathematical models and logistics chains. We found that if you aim for an optimal planning, then often the whole logistics chain becomes instable, and even small delays can lead to big problems. The event with Ever Green was a very big disruption, hence it was expected that it would have a global impact. What is surprising in our research is that also small, seemingly innocent, delays can lead to big disruptions. And this has been observed in various practical occasions in the past. However, this weakness shouldn’t deter us and make us question our technologies. On the contrary, it gives an opportunity to investigate this phenomenon and find ways to adapt our systems. It shows how important it is to keep doing research and being critical about the methods we use in our daily lives. By being critical and patient we can keep improving them. Our new research shows that small adaptations in an optimal schedule can help make logistics chains more resilient to such cascading effects. Moreover, we can compute how an optimal schedule should be adapted. The general take-away message? We shouldn’t get obsessed with optimality; often it is better for everyone to leave some slack!
In what follows we take a deeper look into logistics chains, how local delays can have a global effect, and how we can adapt systems such that the effects are absorbed smoothly.
The ”just-in-time” model
In this model all the steps in the logistics chain can be scheduled in an optimal way such that everything is at the right place on the exact right moment. If someone can guarantee that all parts needed to make a car can be delivered exactly when they are needed, then the factory doesn't need to keep buffers, say mechanical parts, tires, or seats in stock, for the case something is not delivered on time. We use the example of a car factory, but you can imagine that the scenery is similar in the manufacturing of computers, smartphones, televisions, in restaurants and catering, or in airports and train networks. In the latter two, for example, you want to optimally schedule flights or train departures. In this case, the buffer involves the time between departures.
In general, in a logistics chain the buffer is the stock of products, people, or time, so that you can absorb delays when things go wrong. Having large buffers means that the system can absorb delays, but they come at a cost. You need to hire more people or store products in advance. Keeping the buffers small and optimizing the logistics chain leads to lower costs, and hence more profits. In an optimal world, where everything runs smoothly, buffers are just an unnecessary expense. There is, however, a risk hidden in this effort to achieve optimal coordination and efficiency, and you have probably all experienced this in practical situations. Many of you may have experienced the following annoying situation: you want to fly back home and the flight has a delay of 30 minutes. You all board the plane, and then the pilot says that they lost the landing slot at the destination, and you must wait for 2 more hours for a new time slot. But you must wait in the airplane, ready to depart if an earlier slot becomes available. In this case, a delay of 30’ cannot be absorbed in the schedule of departures and landings. The buffer is smaller than 30’. Having such a small buffer means airports can schedule more flights in a day. The downside is that delays can’t be easily absorbed. And of course, if something like this happens there is not enough water and food for everyone on the airplane because that buffer is also optimally scheduled, to avoid additional waste for example.
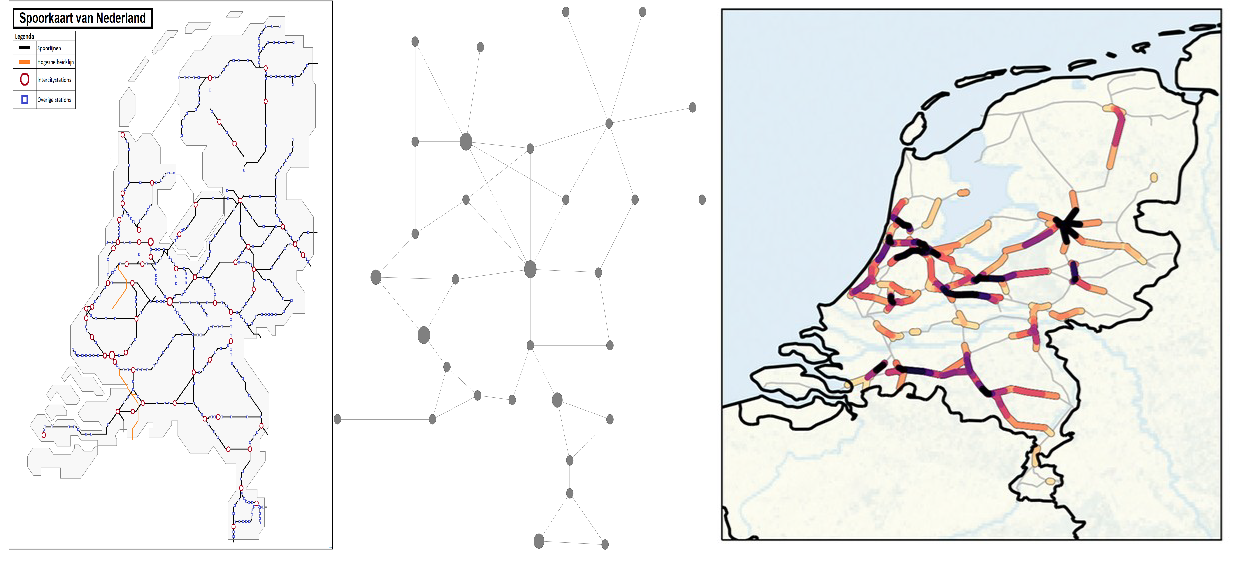
Keeping buffers small, not only in physical stocks but also in time, makes the whole logistics chain very sensitive to unexpected disruptions and delays. Even worse, sometimes even very small, seemingly innocuous delays can lead to a huge cascade of delays throughout the entire chain. This has been observed for example with train traffic. In a paper published in 2021 by Dekker and Panja some examples are shown for the railways of the Netherlands, Germany, Switzerland and Italy. The Dutch example dates from January 2018, when there had just been a storm in the Netherlands in combination with an accident in the north of the country. These two events meant a (near) national standstill of all trains for several hours. Why did this happen?
In most countries, railways witness large-scale disruptions multiple times a year. For densely urbanised countries in Europe, like the Netherlands, railway transport is planned at a high frequency to match the extent of urbanisation. In the year July 2017— June 2018, in total 29 days were marked as strongly disrupted days for the Dutch railways, with most of them occurring in November, December and January. This is no coincidence, even though railway companies use icing protection, adjusted timetables and many other precautions to prevent cold weather affecting their performance. But what the researchers (2021, Dekker and Panja) observed on these days is that “while the initial primary delays, caused by external events, could possibly have been quickly resolved, systems’ internal issues cause new secondary delays, converting an initial locally confined problematic event to an amplified near system-wide disruption”. When we plan all steps in a logistics chain to achieve a theoretically optimal performance, then this cascading effect of primary delays can lead to a break-down of the whole system! ).
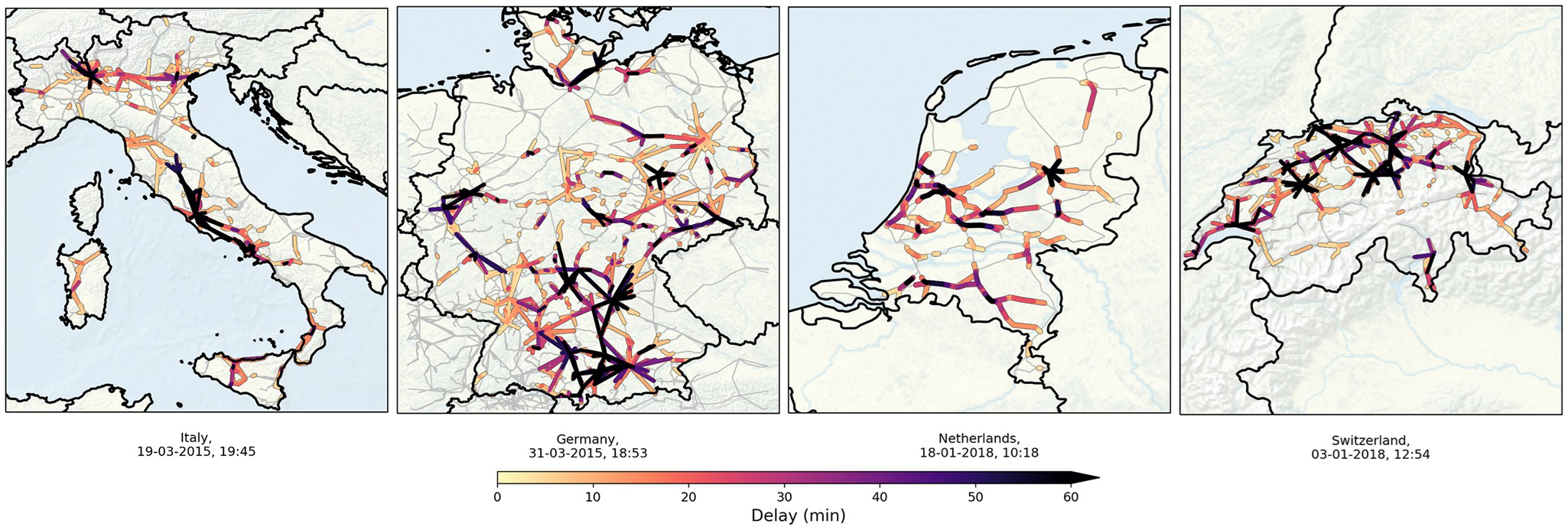
Examples of large-scale disruptions. Railway delays for strongly disrupted situations in four European countries (shown only are the delays larger than two minutes in colours; see SI section A for data description and sources). Panel (a): near-simultaneous occurrence of several problems in the Italian railways in March 2015—a major one around Rome, affecting mostly intercity trains, and one between Milan and Venice. Panel (b): effect of cyclone ‘Niklas’ (31 March 2015) on the German railways. In particular, a specific train near Pegnitz (center-south) was severely damaged by a fallen tree and the rooftop of the Munich station was destroyed, along with multiple smaller incidents across the country. The high risk of more accidents and delays caused the Deutsche Bahn to cancel most of its train activity throughout the day, leaving passengers stranded in major cities like Hannover, Frankfurt, Kassel and Berlin. Panel (c): aftermath of storm ‘Friederike’ in January 2018 in the Netherlands, coinciding with an accident in the north of the country. Fallen trees and damaged overhead lines made the fire department force the Dutch railways to close at multiple stations—resulting in no train activity between the end of the morning and 14:00. A combination of the many disruptions with the lack of resources overview limited the possibility of mitigating delay at crucial corridors. The smaller scale and high density of the railway system in the Netherlands can be recognised also in Switzerland [panel (d)], where in January 2018 (coinciding with storm Burglind/Eleanor in the north-west of Europe) a strong disruption in near Zürich (north) rapidly propagated towards the rest of the country. (Image and caption taken from (2021, Dekker and Panja), under the Creative Commons licence).
The crucial threshold value you should stay away from
In our recent research, published in Nature Physics, we investigated the mechanism behind this cascading effect. Our research into complex logistics networks shows that time buffers cannot be made smaller and smaller with impunity. To understand this phenomenon, we relied on ideas from statistical physics. We found that at a certain, finite, minimum buffer size for the allowed time delay, the entire system goes through the equivalent of a phase transition. Think of an analogy between train traffic and water. When the temperature passes the critical threshold of 0 degrees Celsius a phase transition takes place, water goes from one state (liquid) to another state (solid). And this transition is not smooth, it is abrupt. Phase transitions occur very often in nature, in matter when the temperature or pressure change, in magnetism, in the formation of chemical compounds, or in neural networks in our brain. Such transitions from one state to another are described and modelled using techniques from statistical physics, mathematics, and networks. In our research, we show that phase transitions also occur in logistics chains.
Generally, when studying phase transitions, there is a “control parameter”, such as the temperature in the case of water molecules. This parameter describes the balance between long-range forces, which favour larger scale structures (such as ice crystals in water), and short-range forces from collisions due to random motion. At a particular value of that control parameter, the phase transition takes place. In the case of molecules, it is a transition from gas to liquid, or from liquid to solid (or vice versa). The physics of phase transitions, applied to logistics chains, shows that the temporal buffer size acts as that control parameter, and the equivalent of the temperature of solidification (freezing), is the critical buffer size. In analogy with many physical systems, even just above that critical limit for the buffer size, a system becomes extremely sensitive to even small perturbations. This means that small delays on a local level, make sure that the whole network makes a transition for a “fluid” state, where everything works smoothly, to a rigid “frozen” state, of a nationwide shut-down.
In part 2 of this series we will show the basic mathematical concepts we used to analyze logistics chains, and discuss how phase transitions emerge when analyzing them. In part 3 Frank Pijpers will discuss some personal experiences and ideas regarding interdisciplinary research. Stay connected!
How is it possible that bikes are so perfectly spread out that they are available from almost anywhere? Who are these bike fairies that distribute them evenly across the city? Continue reading if you like to find out who they are and what type of mathematics is involved.
We want our guts to be filled with a diverse range of mutually beneficial and competitive interactions, a perfect blend of friends, frenemies, and enemies to keep our guts active and body on its toes. Read how networks can help understand these interactions!
If, after reading the title, your immediate response is to shout "1/6-th", then you have correctly answered the question. Well done! However, in this article we will focus on the meaning of this question. What exactly is this "chance" of which you've just exclaimed it equals 1/6-th?
One of the main building blocks of modern AI-tools are artificial neural networks, abstract models inspired by the structure and functions of biological neural networks which enable machines to "learn". In this article, I will discuss some thoughts on this topic.
