Mr Markov playing Snakes and Ladders

Until 1999 all Monopoly boxes included an instruction booklet where a short history of its invention is presented. American Richard Brace Darrow (1889-1967) was a self-made man who loved to tinker in his basement, when, after a while, he came up with what we now know as Monopoly and sold it to Parker Brothers in 1935. There is, however, one problem with this story. Darrow didn’t actually invent the game.

Lizzie Magie (1866-1948) was an American progressive writer, feminist and game board designer who was dissatisfied with the inequality between men and women in society. She was also a Georgist: somebody who believes ownership of nature is not possible; it should belong to everyone, equally. Magie wanted to create a board game that promoted the principles of Georgism. A game she would call ’The Landlords Game’.

The Landlords Game is what we now know as Monopoly, but Magie actually included two sets of rules. One set emulated the Georgist system, where players would try to produce equity. Wealth was evenly distributed, and winning was a collaborative effort. The other set of rules emulated a capitalist system, with the rules of Monopoly as we know them today. You can only win by crushing your opponents and obtaining a literal monopoly. Magie tried to sell the game to Parker Brothers, but they declined deeming the game 'too political'. Darrow learned about The Landlords Game through a friend and sold the game to Parker Brothers in the 1930's, only including the capitalist set of rules.

Monopoly has now sold over 275 million units worldwide, making it one of the most popular board games of all time. I am sure that the best strategy to win Monopoly has been discussed and debated on many game nights. Luckily, we can use mathematics to obtain the optimal strategy, so you can use it to beat your family and friends in Monopoly!

But before we explore the optimal strategy of Monopoly, we have to look at another classic: Snakes and Ladders.

Snakes and Ladders is easier to analyze than Monopoly for two reasons. Firstly, it is less complex than Monopoly. There are no Chance or Community Chest cards, and there is no jail. Secondly, Snakes and Ladders is a game of pure chance: there is no strategy involved. The only way to win the game is to simply be lucky. This makes for a game without any strategy, which makes it easier to analyze. This analysis will give us some tools (spoiler: probabilities, matrices and Markov chains) to explore the strategies of Monopoly later on. And in case you are in a phase of orienting for a study in a technology or science related field it is good to know that the mathematics we will show is very important and is typically discussed in the first year of such studies ;).

Snakes and Ladders

Snakes and Ladders (or sometimes Chutes and Ladders) is a game for two or more players played on a 10x10 grid where every square is numbered. Since the two players don’t affect each other’s gameplay, we might as well analyze the game when a single player is playing it.

Since Snakes and Ladders is a game of pure chance, there is no strategy to the game, only hoping. Then what is there to analyze? Well, we can calculate how long we expect the game to go on for: how many turns do you need on average
to get to square 100 and win Snakes and Ladders? This analysis will give us some tools, which we can later use to determine the best properties to buy in Monopoly!

In Snakes and Ladders we use a single die. This means that every number from 1 to 6 is equally like to come up when we throw it. Since there are a total of six possible outcomes on a die, they all come up with probability $1/6$ . We call this a uniform probability distribution. All possible outcomes of the die are equally probable.

The game always starts on square 0 (outside the board). This means that after turn 1, Player 1 has a probability of $1/6$ to end up on square 1, a probability of $1/6$ to end up on square 2, etc. But there are ladders on some of these squares! There is a ladder from square 1 to square 38, and a ladder from square 4 to square 14. Since we immediately go up a ladder when we land on it, we never end our turn on square 1 or square 4. So if we start the game then we actually go to square 38 with probability $1/6$ and to square 14 with probability $1/6$ . We never end a turn on square 1 or square 4, so the probabilities to end up there are 0.

We can summarize all this information in one big table, a matrix. This matrix will contain all probabilities from going to a certain square to another. In the case of Snakes and Ladders, there are 101 possible positions, since we start on square 0 and end on square 100. This means we need to build a $101\times101$ matrix, where the entries encode information of going from one square to another. For example, the first row of this matrix will contain all probabilities of going from square 0 to all other squares, which we discussed above. And the second row will contain all probabilities of going from square 1 to all other squares. But since square 1 has a ladder taking us to square 38 all these probabilities are 0. If we hit square 1 we take the ladder to square 38.

	0	1	2	3	4	5	6	...	14	...	38	...	98	99	100
0	0	0	1/6	1/6	0	1/6	1/6	...	1/6	...	1/6	...	0	0	0

Then, in the next turn, row 38 gives the probabilities for this square:

	0	...	39	40	41	42	43	44	...	99	100
38	0	...	1/6	1/6	1/6	1/6	1/6	1/6	...	0	0

Similar to ladders you can also end up on a square with a snake, which takes you back to a previous square. Using the game board above, can you fill in the tables for squares 5 and 59?

	6	7	8	9	10	11	12	...	10	11	12	...	98	99	100
5								...				...

	18	...	60	61	62	63	64	65	66	67	...	97	98	99	100
59		...									...

If we do this for all squares on the board, we get the huge matrix below! One important rule is that to finish the game, you have to throw the exact number to get to 100. If you throw more, you stay where you are. This is why the probability to go from square 99 to square 99 is $5/6$ . Can you see why the entire row corresponding to square 97 is all zeroes?

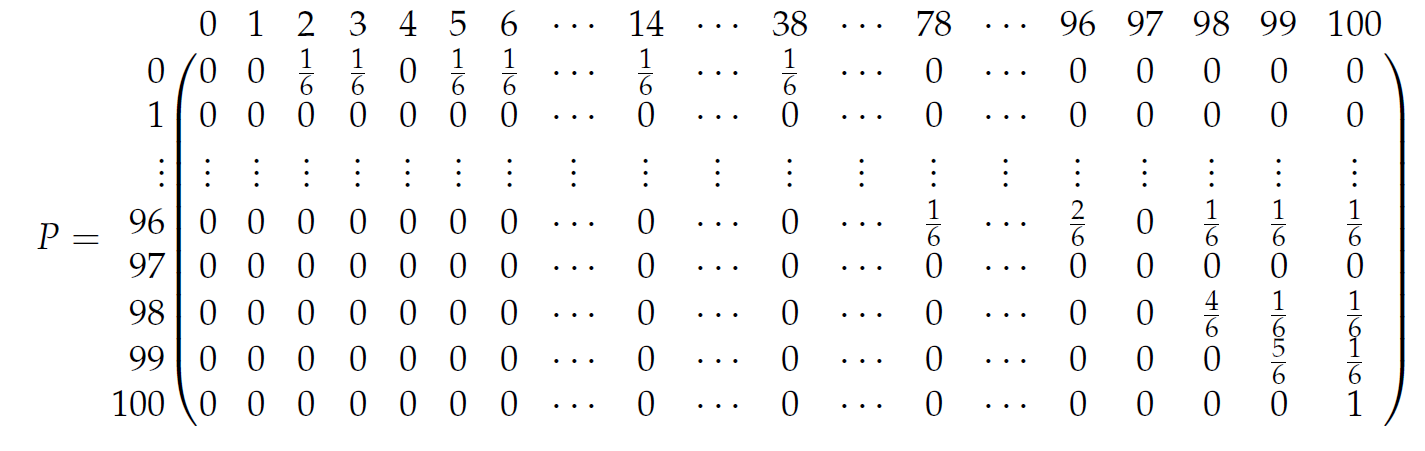
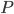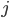The matrix $P$ contains all probabilities to go from square $i$ to square $j$ . This probability is found at position $(i, j))$ .

This is all nice and interesting, but what can we do with this? The matrix P is called the transition matrix, and it represents the probability distribution of a single turn, i.e. the probability of going from any square on the board to any other square. However, in the game we throw the die many times: how do we model that? For people working in disciplines where mathematics plays an important role matrices are very familiar, they are like generalizations of numbers. An important property of matrices is that we can define an addition and a multiplication, just like with numbers. You don't need to know how these work, just that it is possible. But if you are curious and want to see how it works don't hesitate to have a look, it is a little bit technical but doable. And since multiplication of two matrices can be defined, it means that also taking powers of a matrix can be defined! These powers give the full solution to how a game will evolve!

It turns out that if we square this matrix, we get the probability distribution of two turns! In general, if we want to know what the probability is from going to square 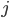$i$ to square $j$ in turn 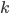$k$ , we can look at the matrix $P^k$ , and look at the number in row $i$ and column $j$ .

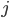How can we use this to calculate the average number of throws needed to finish the game? We know that 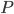$P$ represents the probability distribution of the first throw. We can look at the entry corresponding to going from square 0 to square 100. This is the number in the first row and in the last column. Obviously this probability is 0, since we cannot go from square 0 to square 100 in a single throw.

But what about two throws? As we have seen previously, if we square the matrix, we get information about the probability distribution of two turns. We can look up the entry corresponding to going from square 0 to square 100, but will also be 0, since we cannot go from square 0 to square 100 in just two turns. You can maybe try to figure out yourself what is the least amount of turns in which a player can complete the game.

We need to keep going, now we have to cube the matrix 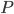$P$ to see the probability distribution of three turns. After that we also need four turns, and five turns, and six turns. This is in infinite amount of work! Luckily, there’s a neat mathematical trick that can help us.

Intermezzo - Did Mr Markov play Snakes and Ladders?

To compute how many rounds a player needs, on average, to reach the final square I rely on two very important fields within modern mathematics, linear algebra and Markov chains (named after Russian mathematician Andrey Andreyevich Markov (1856–1922)). Linear algebra is the area in mathematics studying matrices, like 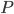$P$ above. Markov chains actually relies heavily on linear algebra and probability theory, but because of the rich ideas it has produced, and its importance in various other fields and applications it has become a research area on its own. All the results I will use later originate from the field of Markov chains. Although I find it really exciting to discuss all of these results in detail, I will just mention them and you have to believe me they are true. Markov chains are so interesting that learning more about them is motivating enough to study mathematics! If you are interested you can have a look at this article written by Nelly Litvak.

Back to Snakes and Ladders

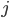Before the intermezzo, we had the matrices $P, P^2, P^3, \ldots$ which give the probabilities you reach square $j$ starting from square $i$ in $1, 2, 3,\ldots$ turns. What we want is the expected number of turns to reach square 100 starting from square 0. To find this we need all the probabilities that you can reach square 100 in $1, 2, 3, 4,\ldots$ steps, these are exactly the numbers in row 1 and column 101 of the matrices $P,\, P^2,\, P^3,\, P^4,\ldots$ . We denote these probabilities by

$p_{0,100}, \, p_{0,100}^{(2)}, \, p_{0,100}^{(3)}, \, p_{0,100}^{(4)},\ldots.$

Mathematicians working on Markov chains have proven that the expected number of turns to reach square 100 starting from square 0 is equal to

$\frac{1}{p_{0,100} + p_{0,100}^{(2)} + p_{0,100}^{(3)} + p_{0,100}^{(4)} +\ldots}.$

Such results carry the name $``$ times to absorption $"$ if you want to read further. But how can we compute this number? In the denominator we need to add infinitely many probabilities! Here comes the creative idea offered by linear algebra!

First we rephrase the problem slightly. Instead of looking up the correct probability in all the matrices, $P, P^2, P^3, \ldots...$ and so on, separately, and adding them, we can also first add all these matrices, and then look up the correct probability! So we need to calculate

$P + P^2 + P^3 + P^4+\ldots .$

and then look at the value in the first row and in the last column. You will wonder, instead of adding up infinitely many probabilities you are adding up infinitely many matrices. This is still a lot of work to do. But watch what happens when we multiply everything by 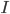$(I - P)$ ( $I$ is the identity matrix, don't worry too much about it, think about it as the 1 for matrices. When you multiply a matrix with 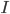$I$ you get the same matrix).

$(I-P)(P+P^2+P^3+P^4+\ldots) = (P+P^2+P^3+P^4+\ldots) - (P^2+P^3+P^4+P^5+\ldots) = P .$

With some rearranging, we get

$(P+P^2+P^3+P^4+\ldots) = (I-P)^{-1}P.$

Again don't worry too much about what happened here, linear algebra is very clear when we can "divide" with a matrix, as we did here. So instead of adding an infinite amount of matrices, we can simply calculate the matrix $(I - P)$ , invert it, and multiply this inverse with 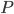$P$ . Then we look up the entry in the first row and last column of that matrix. To do this by hand would take a lot of time. Luckily for us, computers can do it faster. After crunching the numbers, the computer gives us

$\frac{225837582538403273407117496273279920181931269186581786048583}{5757472998140039232950575874628786131130999406013041613400},$