In the previous article Jackie explained to her fried Sam how the problem of picking a card from each of the 13 piles so that there is exactly one card with each rank translates to a problem on bipartite graphs. The mathematical problem asks you to find a perfect matching in a regular bipartite graph. The two friends met for a cup of tea to discuss the solution to this problem!
Sam: Jackie, I am really happy that we will continue our discussion on the puzzle and the problem on graphs! You told me yesterday that you can always find a perfect matching in a regular bipartite graph. Would you like to explain this to me?
Jackie: Sure, I have been thinking quite a lot about the proof of this result and how to explain it without overwhelming you with technical details. Let’s us take the piles considered above and let us try to figure out a way to find such a perfect matching.
Pile 1: A A 3 A Pile 2: 6 6 6 2 Pile 3: 5 5 4 3 Pile 4: 2 5 2 6 Pile 5: 4 3 3 A Pile 6: 2 4 4 5
How would you start with such a puzzle?
Sam: Well, I would start choosing cards from the piles and see how far I come.
Jackie: Ok, let us try it together (you can also try it out by your own while reading the story of the two friends).
Sam: In the first pile I see three times an Ace and in the second pile three times a 6, so I guess I choose an Ace from pile 1 and a 6 from pile 2. If I continue like this, I can choose a 5 from pile 3, a 2 from pile 4, a 3 from pile 5 and a 4 from pile 6. And I have all ranks!
Pile 1: A A 3 A Pile 2: 6 6 6 2 Pile 3: 5 5 4 3 Pile 4: 2 5 2 6 Pile 5: 4 3 3 A Pile 6: 2 4 4 5
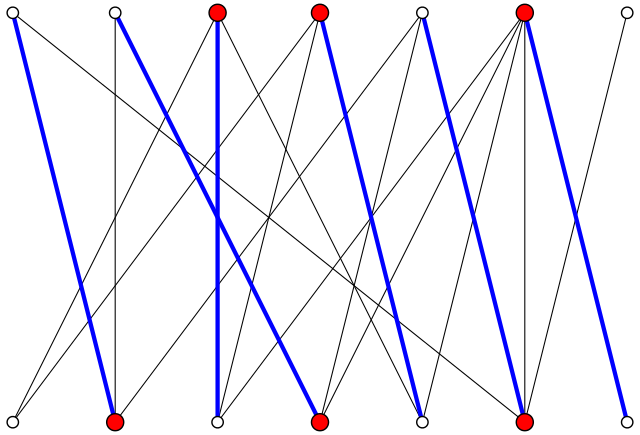
Jackie: And what do you see if you consider the corresponding edges in the graph?
Sam: Hm, that they don’t have any common vertices? And that all vertices are in some edge?
Jack: Great! So, you have a perfect matching. Now the important question, how can be write down a method to always find such a matching? Because you tried it out and you found one. But where could this go wrong? What would have happened if you had chosen Rank 2 from pile 6 instead of pile 4?
Pile 1: A A 3 A Pile 2: 6 6 6 2 Pile 3: 5 5 4 3 Pile 4: 2 5 2 6 Pile 5: 4 3 3 A Pile 6: 2 4 4 5
Sam: Then I would still need rank 3 but pile 4 doesn’t have rank 3 in it.
Jackie: Right, so choosing ranks could lead to a dead end. What would you do to solve this problem?
Sam: I would try to go a step back and change things in other piles, I guess.
Jackie: That is also the main idea of the proof of the result! You start building up a matching until it is finished or until you reach a dead end to a pile that has ranks which have been already chosen. In this case, you must find a way to re-choose some cards from previous piles so that you can choose a new rank from this new pile as well. This mathematical technique relies on a concept called augmenting paths!
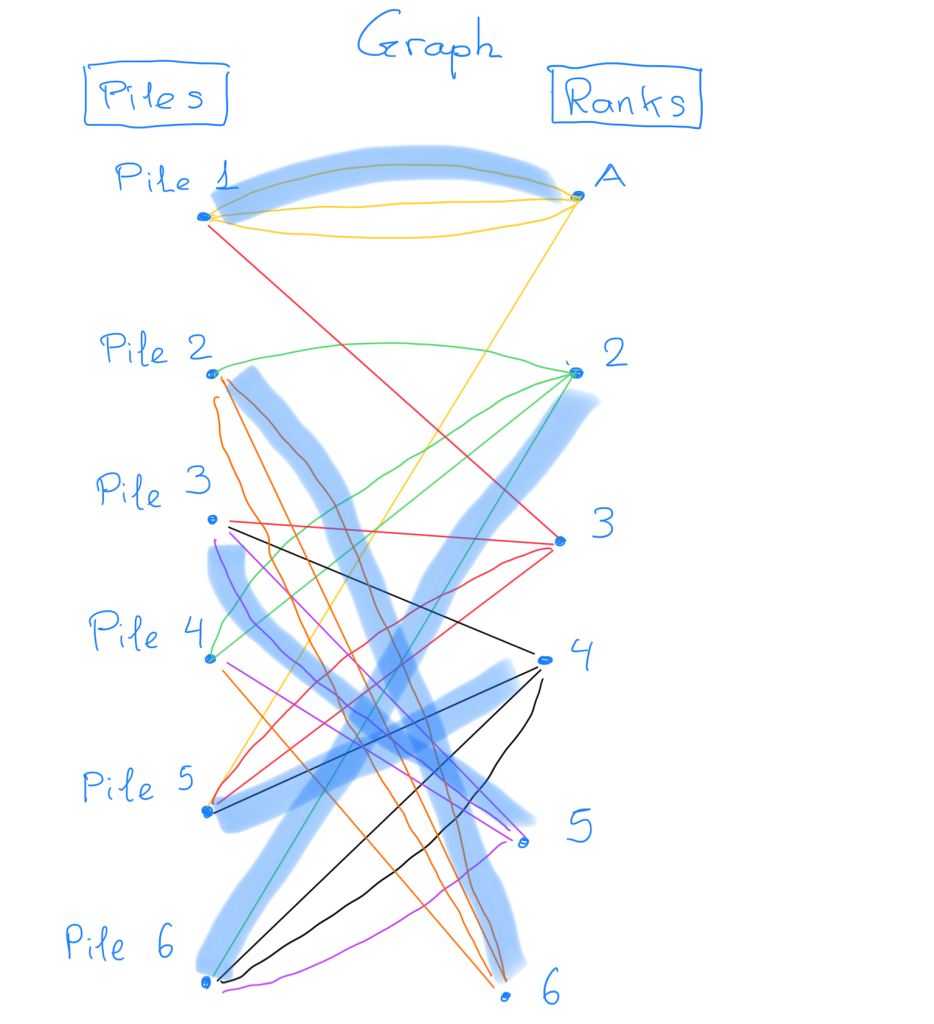
At some point we may reach a dead end. We need Rank 3 but only Pile 4 is available, which has no 3.
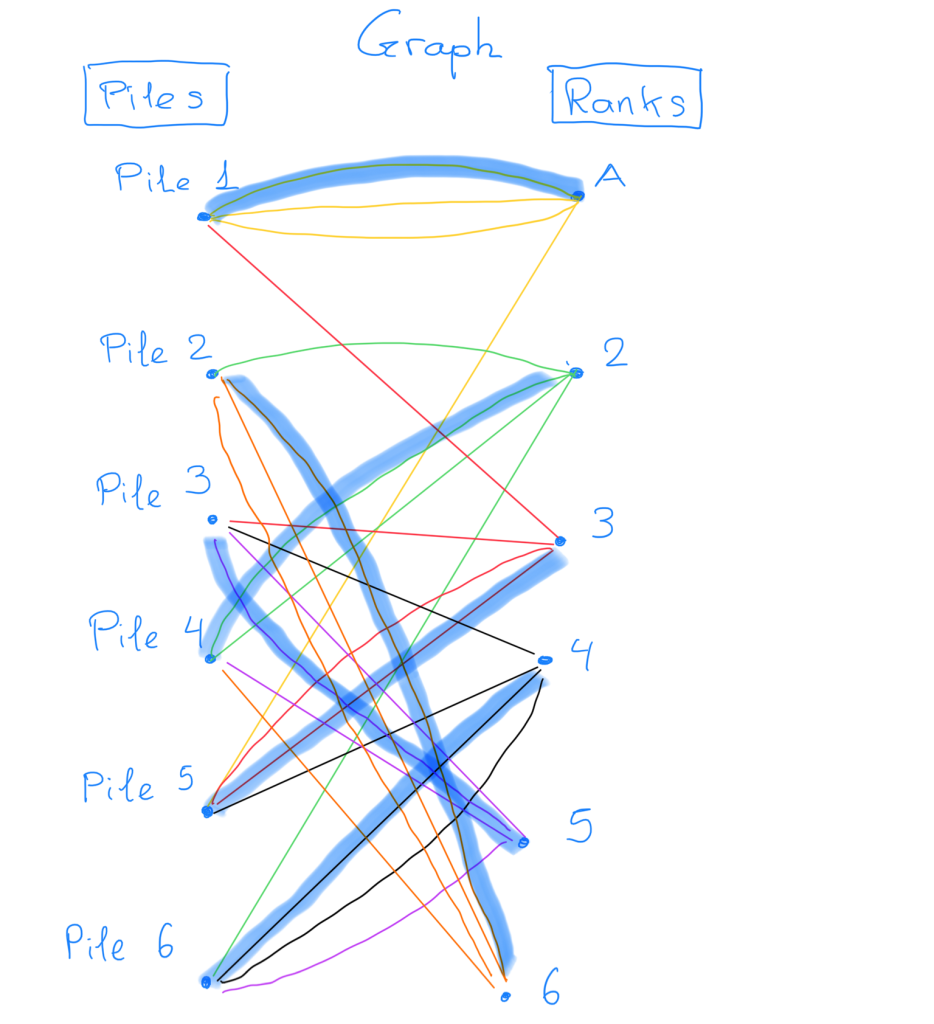
Let’s see how this works. Suppose you start building up the matching and you reach a dead end, like in the case where you choose ranks Ace, 6, 5, 2, and 4 from Piles 1,2,3,5, and 6. Then you are missing rank 3 which is not in pile 4. The way to solve this is the following:
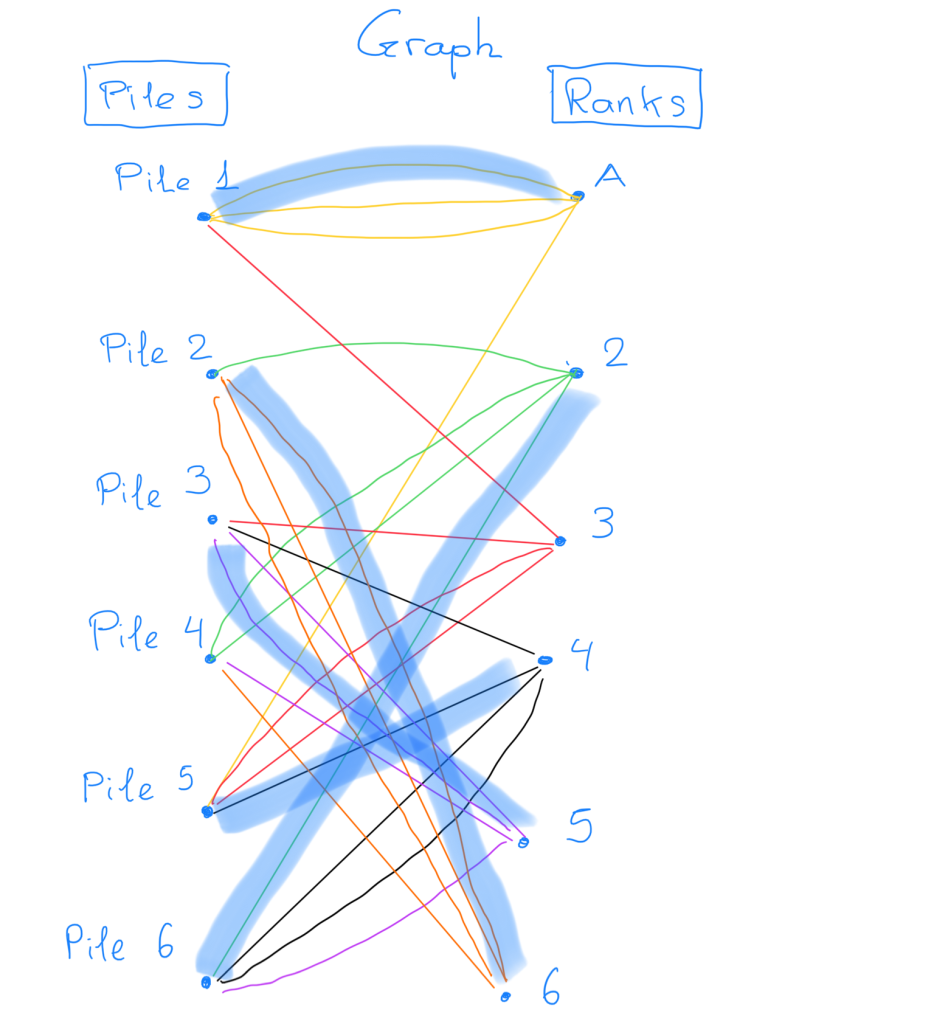
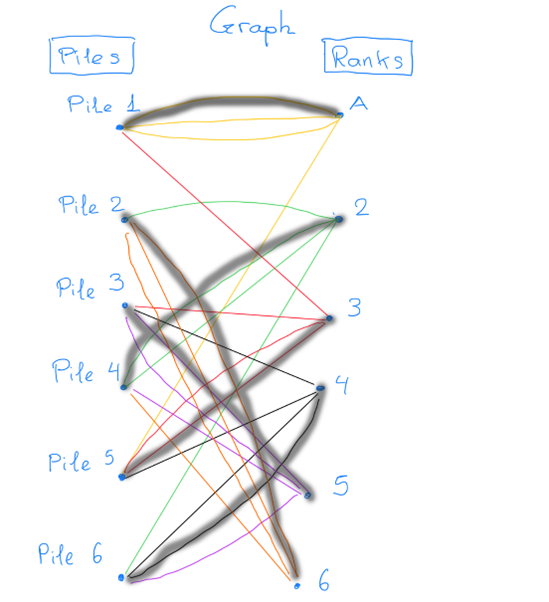
Look at the bipartite graph with the edges you have selected so far. Go to the rank you are missing, in this case Rank 3. You need to find a path using the edges starting from Rank 3 and ending at Pile 4. There is only one additional rule, when you reach a Pile from which a “thick edge” leaves, you must follow this edge in the path. Such a “thick edge” represents an edge that is already chosen in the matching. Let us see how this works in our example.
You need to start from vertex Rank 3, say you use the red edge going to Pile 5. From Pile 5 you need to use the thick edge, this was the rule of the game. This brings you to Rank 4. Say the next edge you choose is the black edge going to Pile 6, from which you take the thick edge to Rank 2. From Rank 2 you can finish the path by choosing the edge to Rank 4. We found a path starting from Rank 3 and ending in Pile 4! Respecting the rule of using the thick edges when possible!
This path starts with a missing rank and ends with a missing pile. It also visits each vertex at most once, and we call the property “self-avoid” in mathematics. Moreover, this path is an "alternating path". You see that in this path the thick edges alternates with not thick ones. We call it the path satisfies those three properties an augmenting path, because it can augment the matching with one more edge. How is this? You need to exchange the thick edges in the matching you had, with the new edges in the augmenting path!
Although you don’t necessarily always end up with an augmenting path when constructing such a path, mathematicians have proven than such an augmenting path always exist once you have a missing rank!
Sam: How do you know that such a path always exists?
Jackie: That is the power of a mathematical proof. You can prove this by a method called proof by contradiction. Assume we have a missing rank, 3 for example. Suppose there is no such augmenting path starting from rank 3. Then all self-avoid alternating paths we can construct starting from the missing rank 3 will eventually end at a rank such that all the plies contain this rank have already appeared in the path before. Construct a subgraph made of all these alternating paths. You must make a couple of observations. First, the number of piles in the subgraph is equal to the number of thick edges in the subgraph. Secondly, the number of ranks other than 3 in the subgraph is also equal to the number of thick edges. Thirdly, for each rank in the subgraph, all the piles this rank can be found in will be part of the subgraph. And the edges connecting them will be in the subgraph as well. But this means that the subgraph will contain one more rank than piles. Since each rank have 4 edges going to it in the subgraph, there will be one pile which will have at least 5 edges going to it. Which is a contradiction!
Sam: So there should be an augmenting path and we can increase the number of cards we picked by one.
Jackie: And this works not only for rank 3, but also for other unpicked ranks as well.
Sam took a sip of tea. Because they talked for so long, the tea was a bit cold. Still, he thought it tasted good, just like the taste of mathematics.
Did you know that if you divide a pack of cards into 13 piles of 4 cards, then you can always pick one card from each of the 13 piles so that there is exactly one card with each rank? There is some beautiful math behind this puzzle.
A mathematician once told me that problems that are very simple to state can be very deceiving, and sometimes turn out to be extremely difficult to solve. One such problem was the Four Color Problem.
A conjecture of Erdős and Hajnal from 1989 says that forbidding any specific substructure results in existence of a very large homogeneous one! In this article you will have a look into one of the most fascinating problems in modern graph theory.
