Random Graphs and Complex Networks: Volume 2 has appeared!

In February 2024, the second Volume of the Random Graphs and Complex Networks book series has appeared. This volume is aimed more towards the research community, including PhD students and researchers, with a mathematical background.
The Elegant Heist: Mastering the Art of Necklace Splitting

Ever wondered how stolen necklaces are tactfully divided? Join us on a captivating journey into the math under necklace splitting! This journey will lead us to a wonderful and very important theorem in mathematics, the Borsuk-Ulam theorem.
The magic of mathematics ♠️♥️♣️♦️
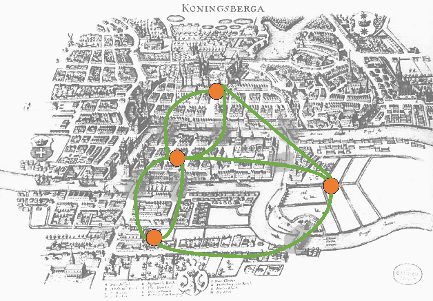
Did you know that a city tour was the foundation of the mathematical field of graph theory? And that graph theory has applications even in magic?
A sparkly new journal for graph theory
Academic publishing is booming, but at what cost? Ross Kang recaps the difficulties and announces a new diamond OA journal in graph theory.
Does no small structure mean larger homogeneous ones?
A conjecture of Erdős and Hajnal from 1989 says that forbidding any specific substructure results in existence of a very large homogeneous one! In this article you will have a look into one of the most fascinating problems in modern graph theory.
Picking up 13 different cards from 13 piles (Part 2)
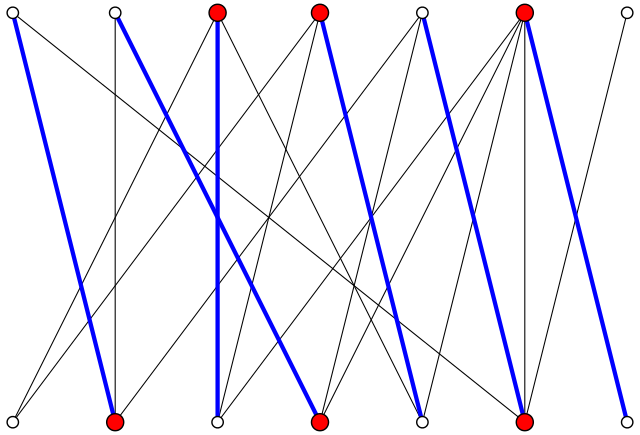
In Part 1 Jackie explained to her fried Sam how the problem of picking a card from each of the 13 piles so that there is exactly one card with each rank translates to a problem on bipartite graphs. The mathematical problem asks you to find a perfect matching in a regular bipartite graph.
Picking up 13 different cards from 13 piles (Part 1)

Did you know that if you divide a pack of cards into 13 piles of 4 cards, then you can always pick one card from each of the 13 piles so that there is exactly one card with each rank? There is some beautiful math behind this puzzle.
Structure is everywhere. So is chaos.

Pick 45 numbers between 1 and 100. Try to avoid creating pairs whose difference is the square of some number and you will fail. Always.
Centrality measures: who is the most important in a network?

In this article, we discuss several ways to quantify the importance of nodes in a network. We will discuss how a simple game can help study this special property, and how it can help us in cases like reducing fake news.
Is it easier to find half a needle than a full needle in a random network?

Common sense tells us that objects of comparable size should be equally hard to find. Yet, when searching inside a random network, surprises are awaiting . . .
