How many colors do you need to color a map?

A mathematician once told me that problems that are very simple to state can be very deceiving, and sometimes turn out to be extremely difficult to solve. One such problem was the Four Color Problem.
Netsweeper: playing Minesweeper without the old-fashioned grid
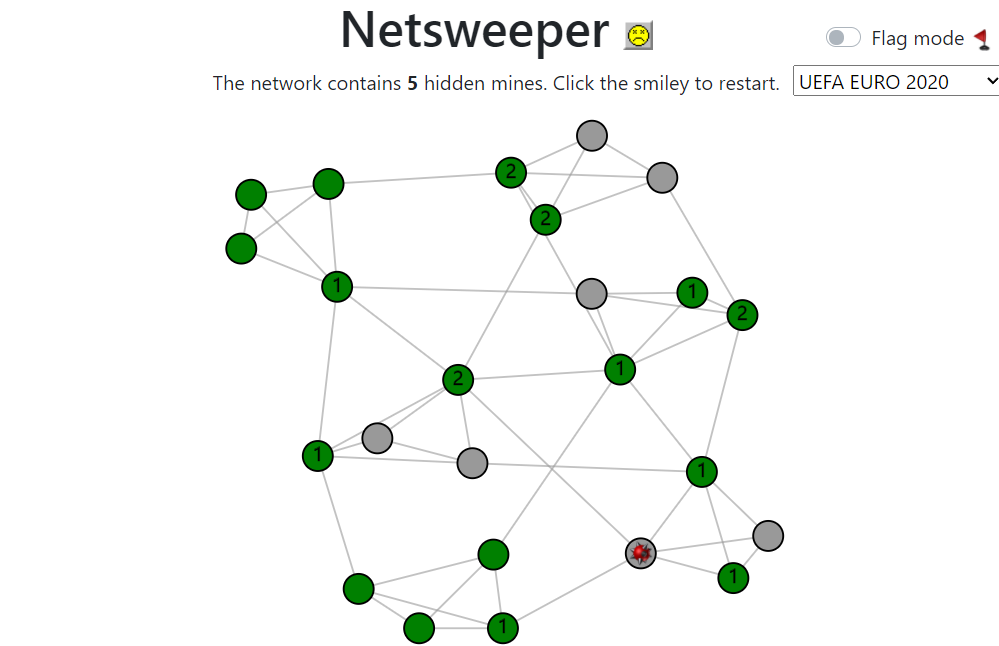
If you were born in the previous century, then chances are high that you have spent quite some hours playing Minesweeper, the classic puzzle game that used to be installed on every computer. In this article, we will present a new network-based version of this game and show how network science can help you play this game.
Percolation theory: about math and gossip

Percolation theory is a branch of mathematics at the interface between probability theory and graph theory. The term 'percolation' originates from materials science. A representative question is as follows. Suppose some liquid is poured over a porous material. Will the liquid be able to make its way from hole to hole and reach the bottom?
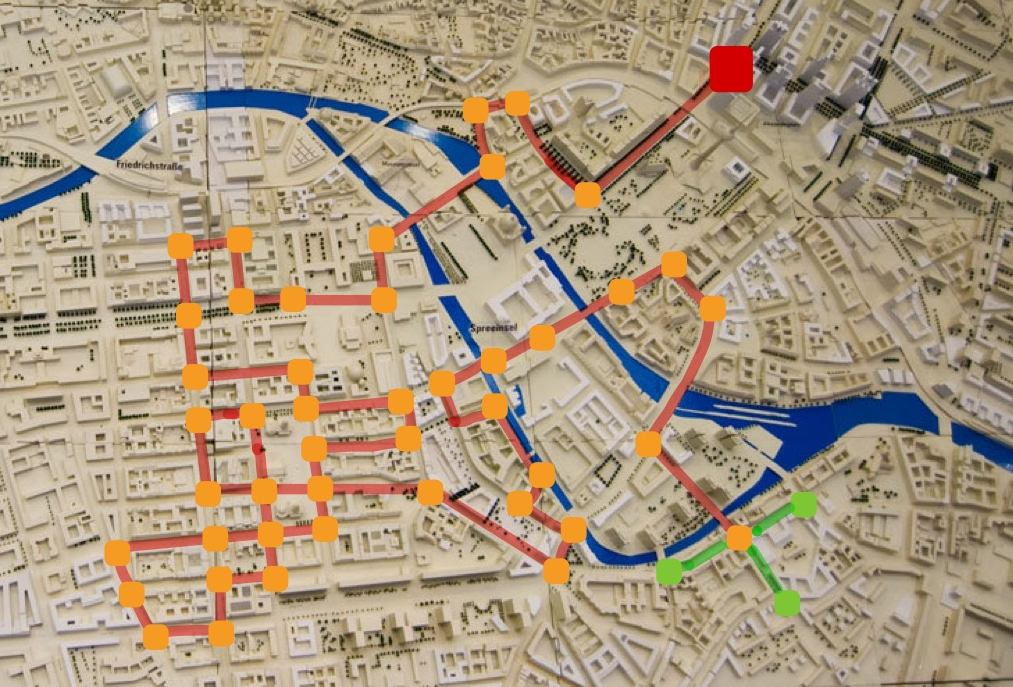
Cycling to 57,912 National Monuments in the Netherlands
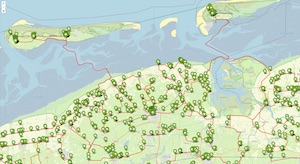
In March 2021 the largest roadmap instance of the traveling salesman problem ever was solved. This is a new record for the Travelling Salesman!
A big breakthrough in the Euclidean Travelling Salesman Problem
Recently there has been a breakthrough in the field of algorithms for geometric network problems, concerning the complexity of the Euclidean Travelling Salesman Problem.
A solution to a long standing conjecture
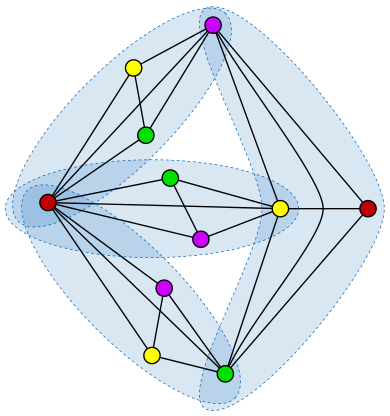
Recently a team of mathematicians has published an article announcing a solution to a long standing open problem in graph theory, the Erdős - Faber - Lovász (EFL) conjecture. This conjecture was formulated in 1972 by mathematicians Paul Erdős, Vance Faber and László Lovász.
Stumbling around in a changing world
Random walks are popularly described as a drunkard’s path down the streets. What happens when the streets also start to move?
Random encounters with Ramsey numbers
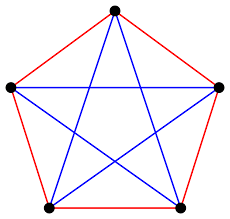
It is was the second time yesterday in a one week time and the fourth in a one month time that I came across Ramsey numbers. In the beginning I thought it was just a coincidence.
Wandering around the bridges!

Can you always find a route through the bridges? This is the question to be answered.
How to plan Valentine’s day using a matching algorithm
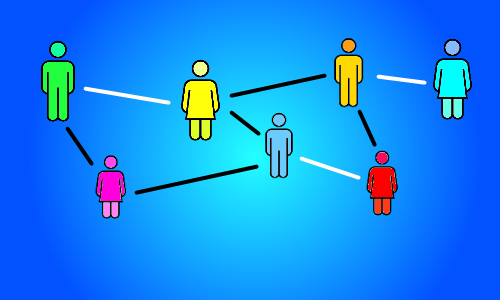
Finding a dating schedule that matches pairs of potential lovers up into dating couples, is an example of an algorithmic problem. There is a clearly defined input, given by the lists of who is considered an acceptable dating partner to whom. It is also clear what we want as the output: a pairing of classmates into acceptable boy-girl pairs that has as many pairs (dates) as possible. How can you find the best dating schedule?
