Abel Prize 2024 to Michel Talagrand
The Abel Committee has awarded Michel Talagrand the 2024 Abel Prize 
for his groundbreaking contributions to probability theory and functional analysis, with outstanding applications in mathematical physics and statistics.
A peek into decision making in service systems
Often due to large waiting times customers abandon shops (online or physical), and owners don't realize that they have left. We call this a loss of opportunity. This is an important concept in queueing theory.
The 100 prisoners escape puzzle
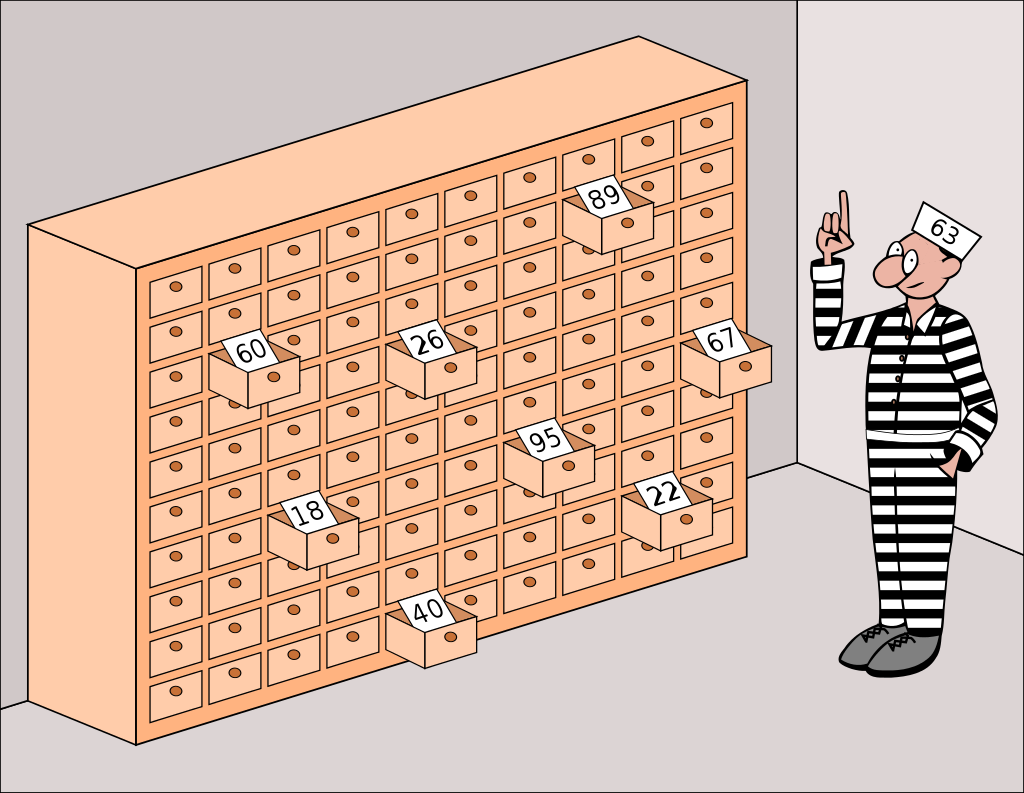
In this article, we will discuss a mathematical riddle that "seems impossible even if you know the answer". It is better known as the 100 prisoners problem.
How do you decide who is the most important?
Imagine you’re in a remote village and only have a limited number of vaccines to distribute to protect the community from a deadly virus, who do you vaccinate?
A difficult decision, but necessary. Assuming that the disease is just as deadly for everyone in the community, the best way to prevent deaths is to contain the spread of the virus.
The share bike mystery
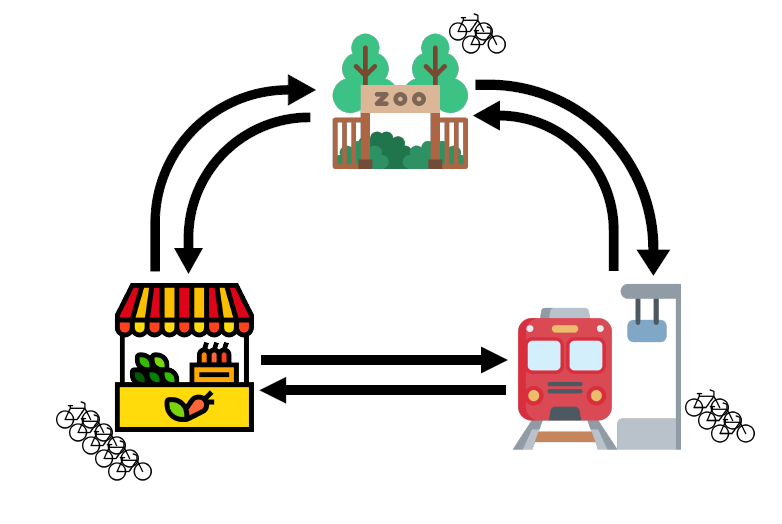
How is it possible that bikes are so perfectly spread out that they are available from almost anywhere? Who are these bike fairies that distribute them evenly across the city? Continue reading if you like to find out who they are and what type of mathematics is involved.
Interview with Marjan Sjerps: Mathematicians have a way of thinking that I really like
The Netherlands Forensic Institute (NFI) has a great deal of in-house knowledge in the field of forensic products, research and services, and provides many organizations in the field of security and law with reliable information from traces. Mathematical models are used within the NFI to understand the evidential value of the traces found.
Percolation theory: about math and gossip
Percolation theory is a branch of mathematics at the interface between probability theory and graph theory. The term 'percolation' originates from materials science. A representative question is as follows. Suppose some liquid is poured over a porous material. Will the liquid be able to make its way from hole to hole and reach the bottom?
Stumbling around in a changing world
Random walks are popularly described as a drunkard’s path down the streets. What happens when the streets also start to move?
Shreds of memories of Paul Erdős
In mathematics it is almost impossible not to encounter the name of Paul Erdős. Much of his work centered around discrete mathematics, cracking many previously unsolved problems in the field.
Large Deviations Theory: understanding the incredibly rare
Probability Theory is one of the most important tools for studying networks. Most things Probability Theory tries to explain are about average or typical observations.