I am thoroughly addicted to puzzles. Sudokus, collaborative exit room board games, Wordle, the Knotwords app, jigsaw puzzles. I always have a puzzle book on me or an app ready for the train ride. As I am writing this I am looking at a stack of board games waiting to be played sitting next to me on my shelf. My absolute favorite kind of puzzle is the Nonogram (or Hanjie, Oekaki Logic, Paint by Numbers, Picross, Griddlers…). You might have seen one before.
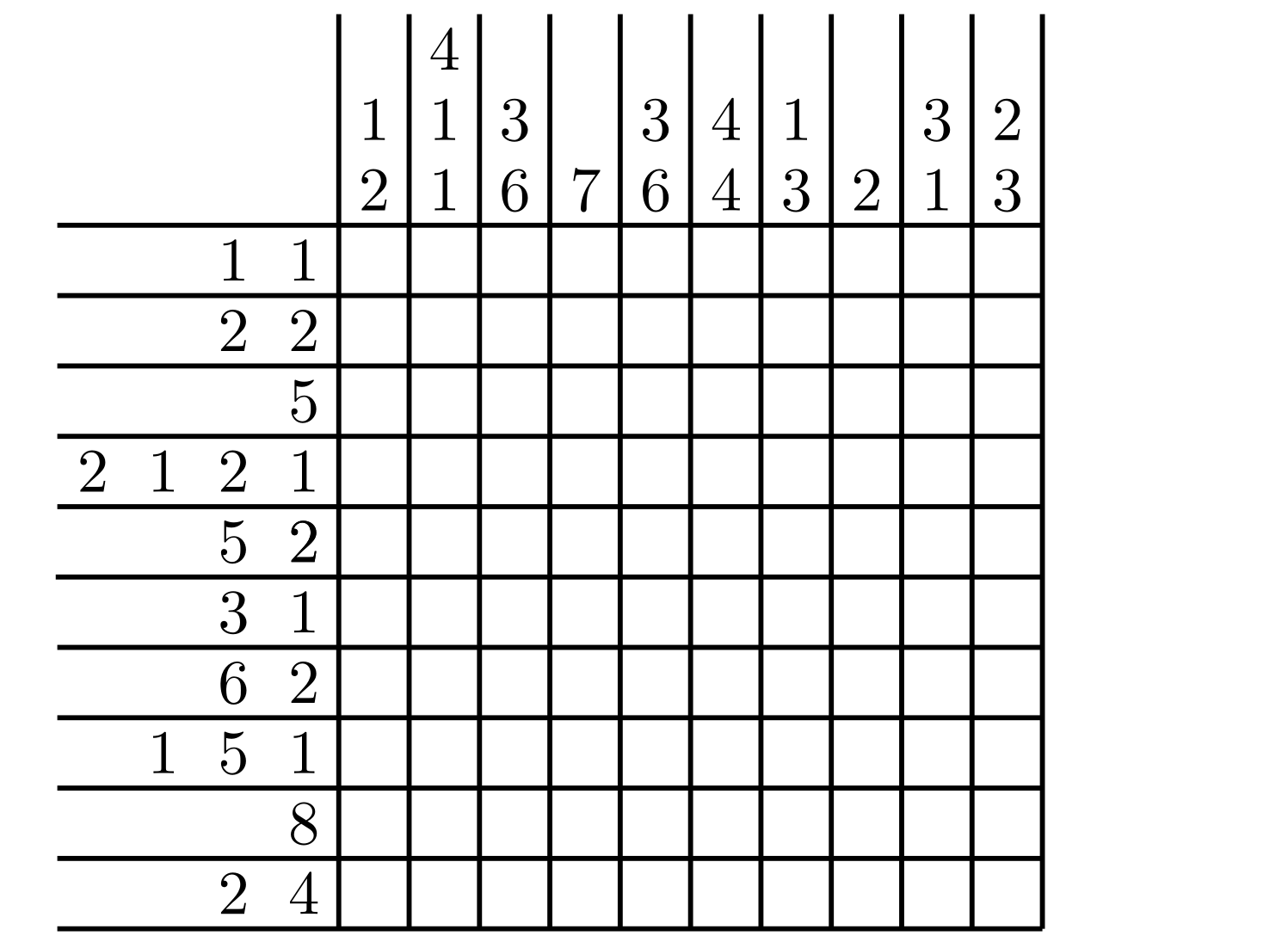
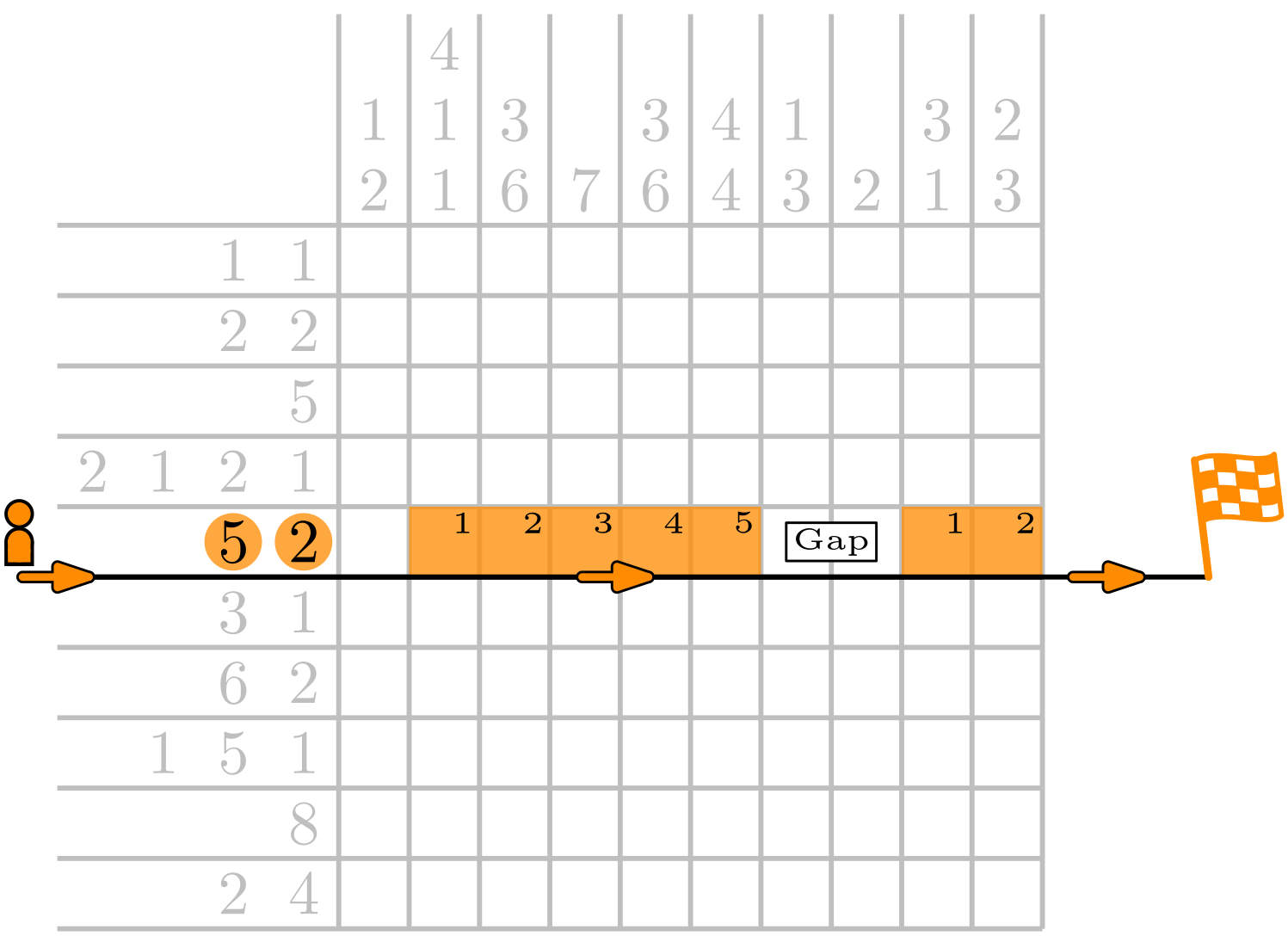
The rules are fairly simple. You get a grid. Every row and column has a list of numbers (or hints). You want to color in the right set of cells and the hints tell you which. A single number in a row (or column) means you have to color in that many cells consecutively in that row (or column). A way to think about this is to imagine that you have the solution and you are walking along one of the horizontal lines from left to right and lets say the hint attached to the line (on your imaginary left) is“5 2”. While walking eastward, if you keep looking to your left you see a number of cells. At some point one of them will be colored in. You start counting how many cells are colored in before you see a blank cell again. One, two, three, four, five, blank! Five colored cells in a row. If you check the list of hints and you can see that matches the first number. So you keep walking and the next time you see a colored cell you start counting again. This time it should be two to match the second number. If this is correct for all horizontal and vertical lines (on both sides), the Nonogram is solved and you’ll have a picture in the grid as the result. Here’s an example.
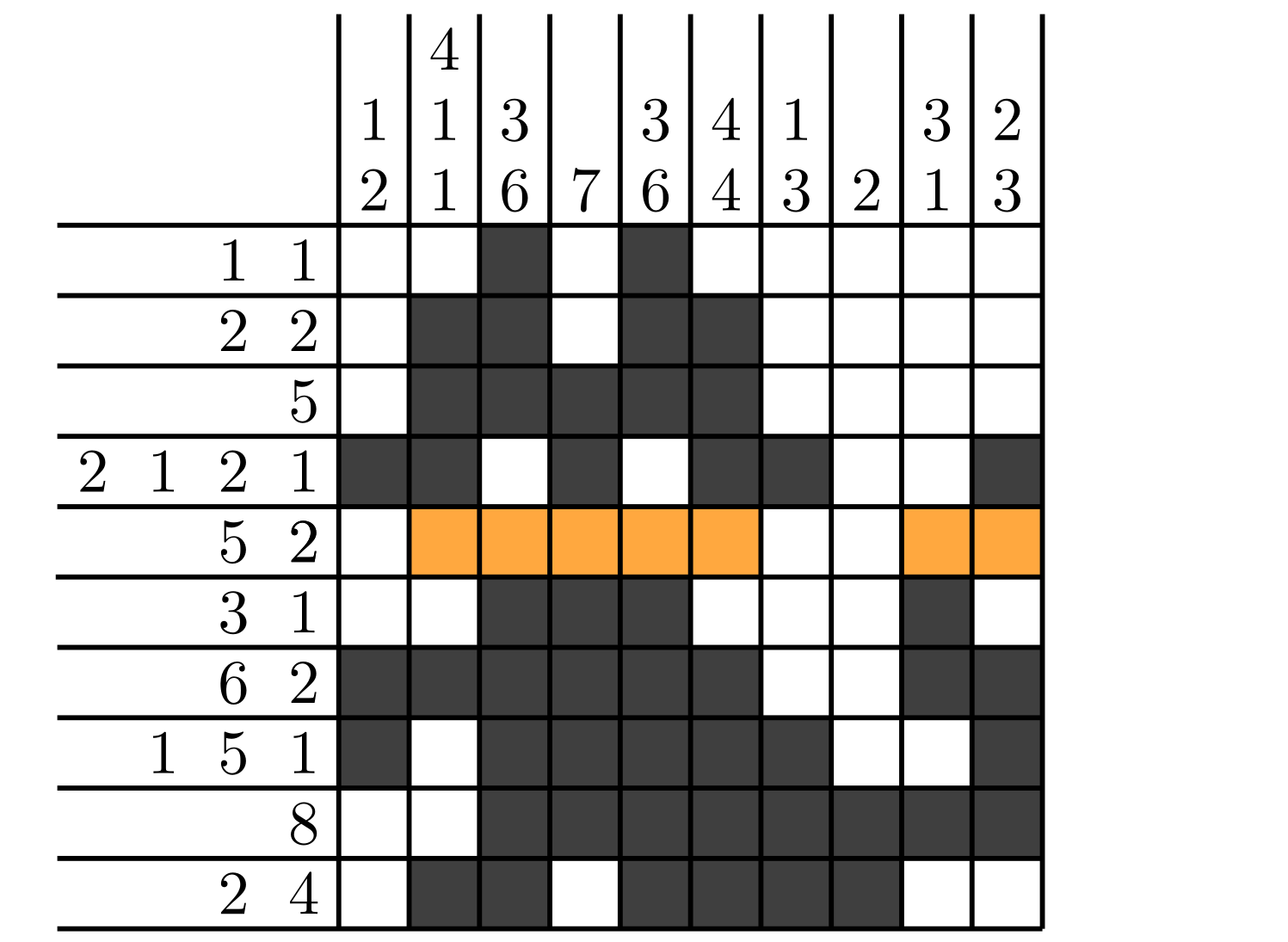
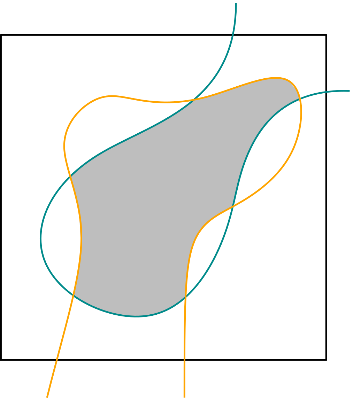
Cool right? A bit pixelated though. Works well for an 8-bit retro image, but what if we want a solution with curves? Let me show you the Curved Nonogram:
Alright, so what’s going on here? It’s not a grid anymore, but we still have various cells and the goal is still to color them in according to some hints. The hints look a bit different here. On the ends of every curve there are small boxes attached to it. They sort of look like little flags and there’s one set of these flags attached to either side of the curve. Now you can again walk along one side of a curve and the counting rule is the same. The blocks of colored cells on one side of a curve should correspond to the hints (flags) on that side of the curve.
In Fig. I we can see the clean puzzle. We will do a very detailed run through on how to solve this puzzle, but you can safely skip the long winded explanation if you want. Just look at the finished puzzle (Fig. XII) and compare how all of the hints line up with the filled in cells.
With that said let’s dive in and let’s look at one of the clues on a curve, namely the clue “6” on the curve highlighted orange in Fig. II. If we imagine walking down the curve and looking on the side of the curve where the clue is (i.e. the side where the small figure stands) we can see 8 consecutive faces (face 1 to face 8 in Fig. II ). The clue tells us that there is a block of six consecutive faces within those which we have to color in. This means our options are 123456, 234567 or 345678. You can see that in every case the faces 3, 4, 5 and 6 are colored in. Therefore we know that we can safely do so, see Fig. III.
Next we can see that the two “1” hints on the blue curves in Fig. IV are now already fulfilled, because they border on an already filled cell. As a consequence we can mark all other faces on these curves (on the side where the hints are) as “not to be colored in”, which I will do by graying them out in Fig. (V). One of the faces we grayed out was face 1 from Fig. II (and Fig. VI). That means that the “6” hint of Fig. II cannot mean that we color in faces 123456. The leftover options both include face 7 and we color it in, see Fig. VII.
Now we turn to the only curve with two hints on the same side, the blue curve in Fig. VIII. Note that the two hints mean that there is a block of two filled in cells and a single filled in cell and that between them there must be at least one gray cell to seperate them. Since there is already a block of two consecutive filled in cells, the “2” hint is already fulfilled and we can mark the cells just before and just after this block gray to indicate that they have to remain blank as done in Fig. IX.
Now we choose a “2” hint on the right side (the curve highlighted in orange in Fig. X). This curve has (on this side) only one colored cells so far. But we actually know where the second cells has to go, since one of the neighboring cells of the already colored one is marked gray. Therefore the other neighbor can be colored in (Fig. XI).
From here it’s easy to complete the puzzle (there is more than one hint that can be used to figure out the last step) and we finally have the solved Nonogram, which is the logo of the Network Pages.
Here’s what I love about curved Nonogram. What do you get when you solve a Sudoku. Well, a solved Sudoku, 81 numbers on a piece of paper. For a crossword? Maybe a word or a phrase. But for a curved Nonogram? You get an entire picture. And not just the pixel version. It might not sound like much but, as I said at the start, they are surprisingly addictive. So this is the point where you might expect me to link to a cool website with more examples, recommend you an app that has all kinds of different curved Nonograms or maybe recommend you my favorite puzzle book on the topic. And I’d love to, but there’s a slight hitch. There aren’t any. I only really know of them because a friend of mine is in the habit of creating holiday themed puzzles as greeting cards and I got one for Christmas.
Let's create a Nonogram!
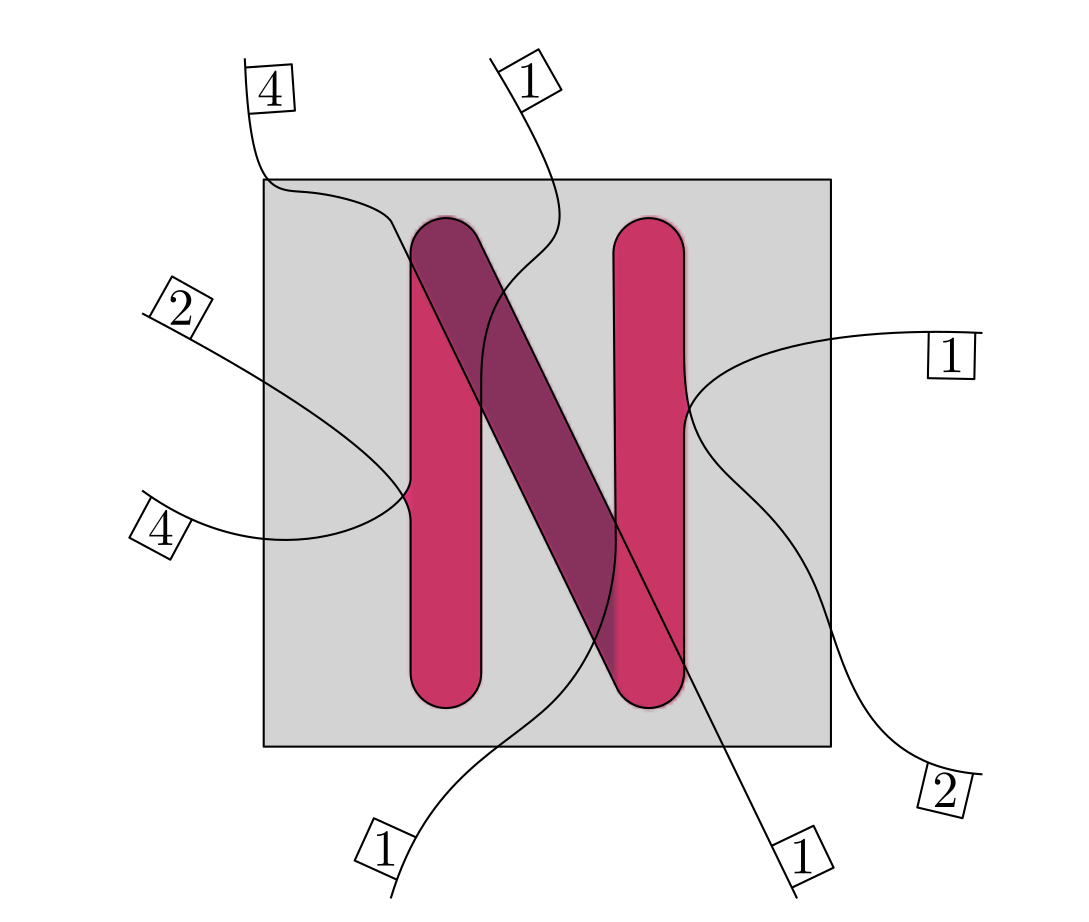
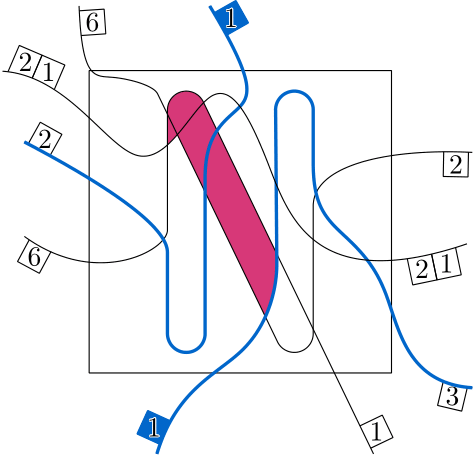
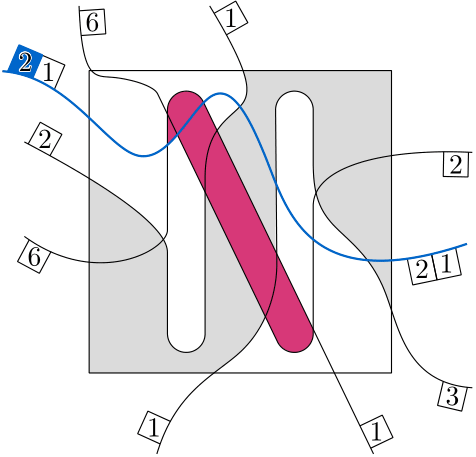
So maybe let’s try to create one together. How hard can it be? Let’s start with an image, that we would like to have as a solution. Something simple, like this picture of a crescent moon below. Then we extend some of the curves, add some additional ones to make the solution less obvious and put the entire thing in a box (middle). I also already placed some of the clues in the figure on the right (I left out the ones that would just say ‘0’). Now only the red curve has to be labeled. So lets do it together. We start at the bottom and walk along it looking to our right. We see a blank cell, then a colored in cell, then blank again, filled in and finally blank again. So by our rules, we would place two clues which both say ‘1’.
But wait a minute, we have not actually seen two colored in cells, it was one and the same. So, do we maybe only place one clue? And if so, should it say ‘2’ then? This is at best unclear and at worst very confusing for someone trying to solve the puzzle.
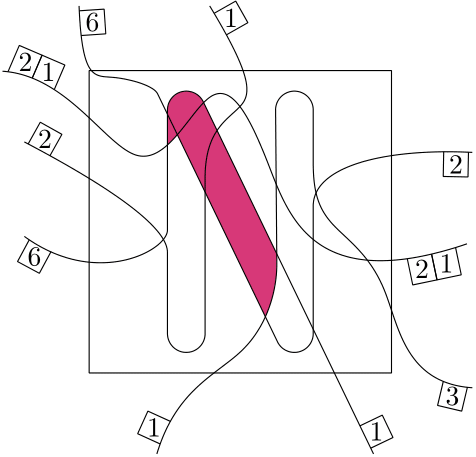
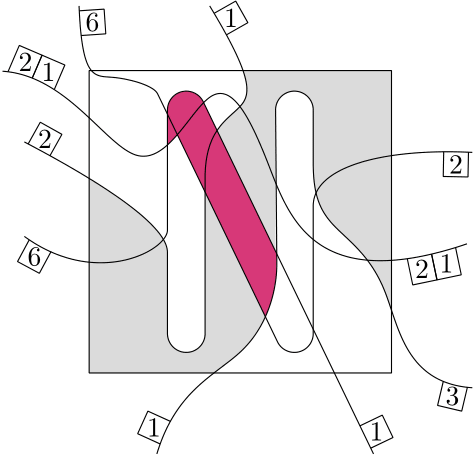
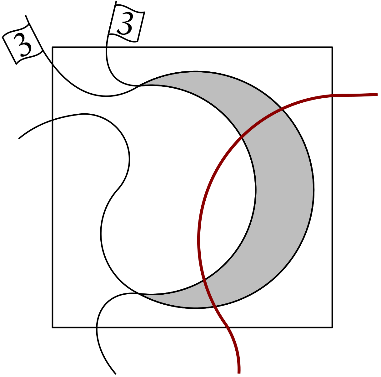
To explain what’s happening we need some terminology (don’t worry this is not where it’s getting technical… At least not yet!). The curves we placed partition the square into cells. Every cell has a boundary which consists of parts of the different curves which form the border of the cell. You can think of the boundary like a fence around the cell. And the problem we have just seen stems from the fact that we have a curve (the red one), which appears more than once on such a boundary of a cell. We call such a cell a bad cell (not very creative I know, but at least it’s easy to remember).
The gray cell is an example of a bad cell.
So we do not want to have any bad cells in our Nonograms. And it turns out that this is a common problem. There is an automated methods to generate curved Nonograms. A large number (about 90%) of puzzles this system creates contain bad cells. So what can we do about that? Well we could move some of the curves but we really don’t want to mess with the figure. So here’s an idea: If one curve appears twice on the boundary of a cell we can try to draw a new curve through the cell to separate the two parts.
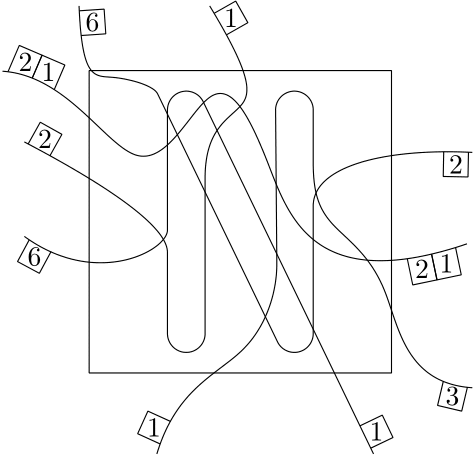
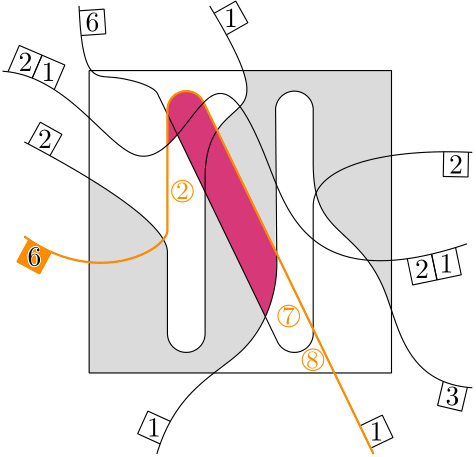
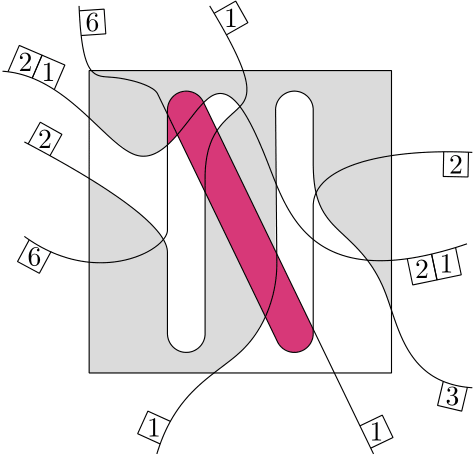
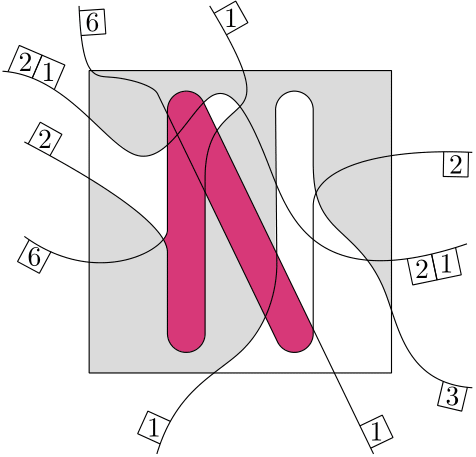
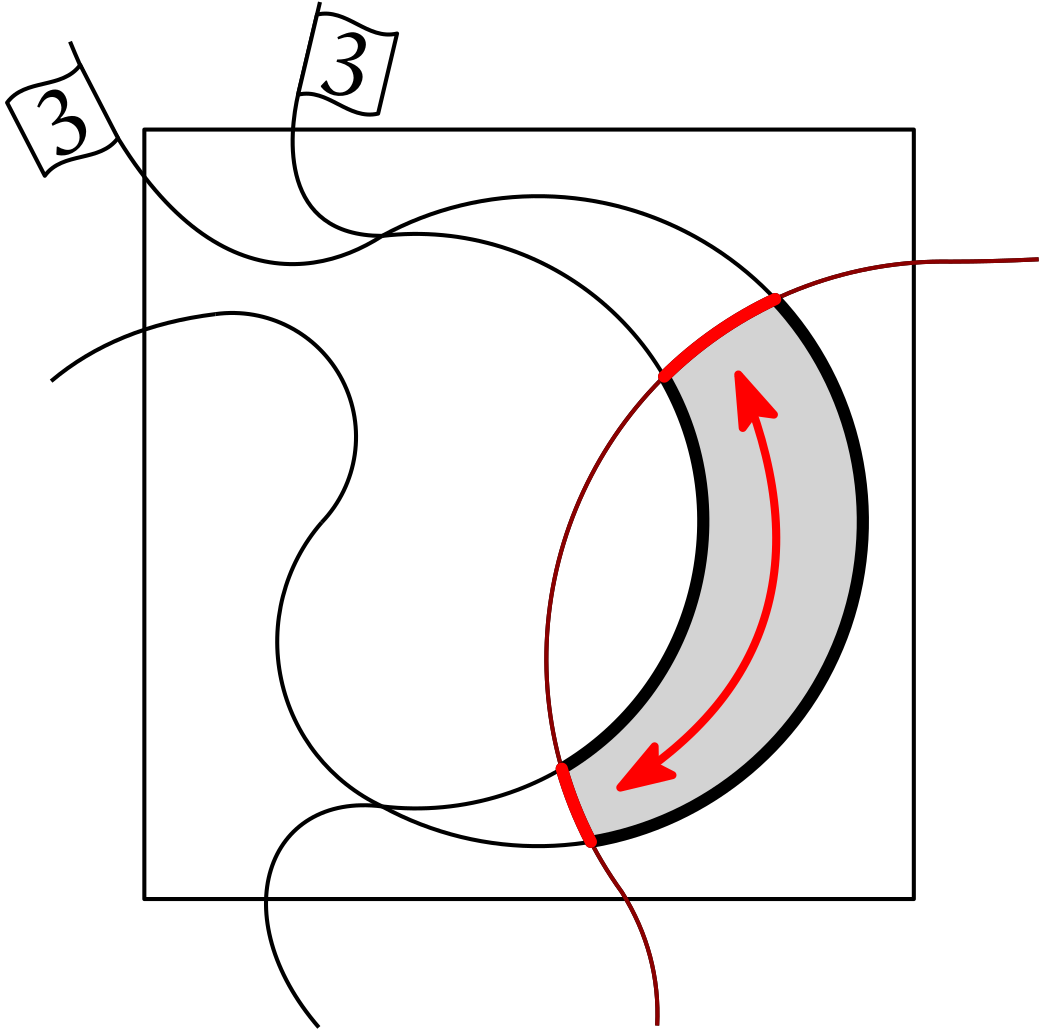
This leads to the following question: Can we just keep adding new curves to make it better? Let’s look at the example again and let’s make it simple. Can you add a single curve so we don’t have any of the bad cells? It’s like a puzzle in a puzzle. A solution looks like this:
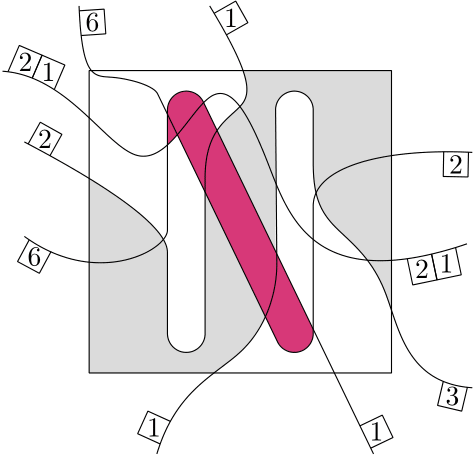
For the small puzzle it kind of works to figure out a solution by hand. (the green curve in the picture above). But what if we go bigger? Look at this version of the same puzzle with more additional curves.
It doesn't even have that many more curves, but it is becoming already very tricky to even find all bad cells, let alone checking if there’s a single additional curve which properly cuts through all of them.
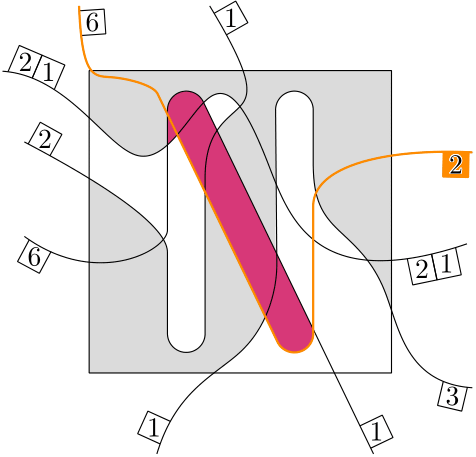
Let me make it a bit easier. Here’s a version where I connected all curve parts that appear multiple times.
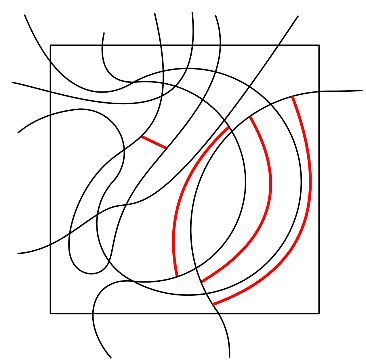
Now it’s a bit clearer and we can reformulate our question: can we add a new curve, which cuts through all of the red connections? To make sure that this is the same as cutting all bad cells into two good ones, there is one more thing the curve cannot do. It cannot go through a cell twice (it would made the cell bad itself).
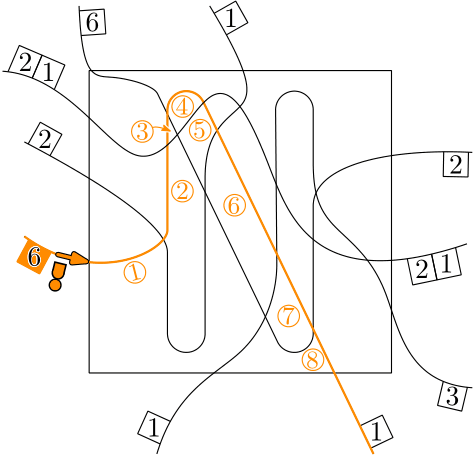
At this point I would like to go on what might appear to be a little tangent, but I promise it becomes relevant later. Let’s look at the solution to the small version again. Or more precisely: at a couple:
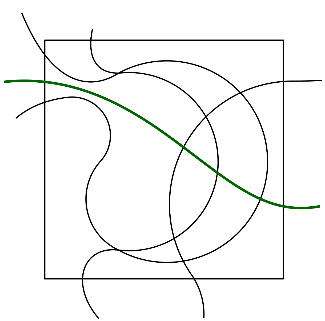
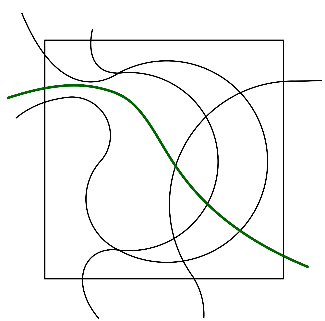
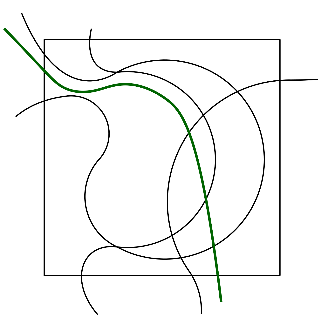
These all look different, but if we break it down they all go through the same list of cells in the same order. And we can try to represent curves added to a puzzle in a way that only uses this information. And we will use Graphs or Networks for this (Hey, that’s in the website name!).
Image putting a dot into each cell. Then connect cells if they are neighbors. For technical reasons the outside of the puzzle counts as one big cell here, but I will ignore that for now. The result is a network called the dual graph of the puzzle and it looks something like this.
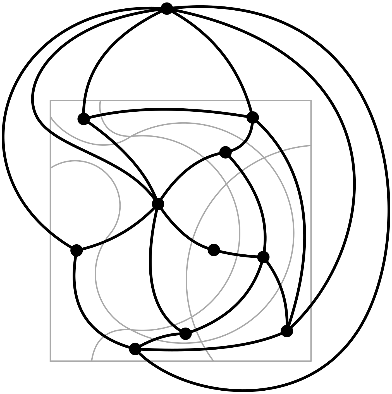
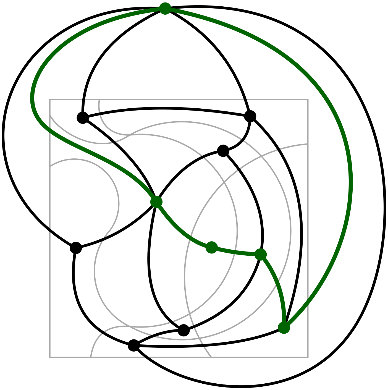
A big loop in this dual graph (usually called a cycle) now represents the order in which any new curve moves from one cell to the next.
OK, that’s a nice tangent and all, but how does it help us? Well let's use this idea of representing a solution as a big loop in the dual graph and state the original problem in that language. We want to find a cycle in the dual graph of the puzzle that visits all bad cells and cuts all red connections (remember that this was the same as a curve that cuts all bad cells into two new good ones).
And wouldn’t you know it, we have successfully taken our puzzle creation problem and have turned it into a question about graphs. For our problem it turns out that we can use a result of Björklund, Husfeldt and Taslaman, who have shown that one can find* a cycle in the dual graph of our puzzle** efficiently*** with a very clever algorithm.
As you can maybe tell by all the asterisks attached to the previous sentence, I might have skipped some details there. If you want to see the nitty-gritty let’s get into it, but fair warning: beyond here there be jargon. If you want to save that for some other time and would like to skip to the end instead, the technobabble stops at the start of the last paragraph.
*: Finding a solution is not actually guaranteed with the algorithm. It has, what is called a one-sided error. In this case this means that if you find a solution, all is good. But if you don’t find a solution there might be a (admittedly small) probability that the algorithm has missed it. The solution to this is surprisingly low tech. Just run it again, every time you do it gets exponentially less likely that you missed something because the probability that you miss the solution k times in a row is the probability of missing it once to the kth power (i.e., something that decreases very quickly). Alright on to the next caveat.
**: Not all puzzles actually have a solution which uses a single curve to eliminate all bad cells. Below is a small example of a puzzle that cannot be fixed with a single curve. The green and the orange curve appear three times on the boundary of the gray cell. It is impossible to properly separate all three parts with a single curve. You can try. Actually trying something for yourself and seeing why it doesn’t work is a pretty good exercise and something that mathematicians do a lot, when they suspect something is impossible (just remember you can cross each cell only once).
And now the last caveat.
***: I used the adverb “efficiently”. Efficiency can mean very different things in different circumstances. If you want to lift a rock need about twice the force for a rock that’s 20kg than for one that’s 10kg. That’s a linear relationship. But if you want to lift a rock that’s double the radius (yes, the rock is a perfect sphere in this analogy), the force will increase with the third power relative to the radius. A cubic relationship.
For computer programs, we (a very narrow ‘we’, which includes a subset of theoretical computer scientists in my particular academic environment) usually measure the efficiency of an algorithm by analyzing how the runtime scales with the input size1. As long as the runtime is a polynomial (and not exponential) in the input size, it is an “efficient” algorithm.
The algorithm of Björklund, Taslaman and Husveldt does not have polynomial runtime. Instead it is exponential, which is bad news. However the part of the input on which it depends exponentially is the number of bad cells. The dependency on anything else is in fact only linear (which is good news). This is known as an FPT-algorthm and they work particularly well if there is a reasonable assumption that the thing on which they depend exponentially (here the number of bad cells) is small relative to the remaining instance size.
1 If you are wondering “how exactly do you measure ‘input size’ of a problem instance?”, that’s a very good question. While I don’t have the space to go into details here, if you’re curious the key word you are looking for is “Turing machines”.
So it seems we can figure out (under some assumptions) how to solve our problem with a single curve. Where to go from here? Well, the natural extension is to use more than a single curve. If you checked out the technical details, you saw an example of a puzzle where we can not take care of all bad cells with a single curve. Can you find a similar counterexample of a puzzle which cannot be solved using two curves? And with that, have fun solving puzzles! Should you stumble over a curved Nonogram in the wild, let me know!
Say you are living in Eindhoven and would like to spend a day in Amsterdam: what better way to get there than taking the train? Before your train departs, a whole logistic operation has taken place in the headquarters of the railway company to make this trip possible.
Have you ever wondered what kind of insights you can gain about games by looking at it using a mathematical lens? In this article we have a look at Snakes and Ladders, and in a follow up article we will dive into Monopoly!
A mathematician once told me that problems that are very simple to state can be very deceiving, and sometimes turn out to be extremely difficult to solve. One such problem was the Four Color Problem.
