Amsterdam is not known for its beautiful weather which means that when the sun does roll in, I try to spend a lot of time at the various swimming spots in the city. Other cities of course offer something like a beach, but whether at the beach, a river, or a gracht, when its time to jump in the water I inevitably ask a stranger to watch my (or my groups) items while I cool down in the water. I place my trust in them to not run away with my cash, phone, or keys and indeed protect these should a third party come looking.
Trust is also required when we buy a used car from a personal connection or via-via. We (used to) accept cookies when browsing without thinking until we learnt that these may indeed be being used against us. Even when we vote for a politician to act in our favour, we trust that they will use their position (gained by our trust in them) to enact policies which are in our favour. In this article we will explore how Game Theory has been used in attempts to model trust and cooperation.
Game Theory: Key ideas
The framework of Game Theory dates back to Hungarian-American mathematician John von Neumann in 1928. Though it was another John, John Nash, who developed the ubiquitous equilibrium construct, the Nash Equilibrium (elaborated upon shortly). Game Theory is concerned with the rational decision making of individuals in the context of a game. Game is a broad term because it can mean a literal game (like chess), but it can also be used to describe any interaction between two or more people who have a variety of courses of action. It is successfully employed by policy makers in the fields as varied as auctions, industrial organization and political science. Academics have also used it to model and predict behaviour of animals and organisms in biology.
In Game Theory, the players are rational individuals take the action which maximizes their (expected) reward. A game is defined by a set of actions available to the players involved and a rule for assigning rewards to the players based on the combination of actions chosen. When games are between two individuals it may be succinctly represented by a game matrix. Take as example the fantasy favourite Boulder-Parchment-Shears, in which boulder crushes the shears, shears cut the parchment and parchment covers the boulder. This game has the game matrix:
Represented in this way, we can easily read off the reward given to either player by looking at the appropriate entry in the matrix. A 1 is the reward for winning the round, a −1, the ‘reward’ for losing and a zero indicates a tie (draw). The individual who chooses their action from the rows, is the row player and similarly the player who chooses their action from the columns, is the column player. The entries of the payoff matrix are ordered giving first the row player and then the column players reward. If the column player chooses to play Parchment, while the row player chooses Shears, we read off the table that the column player gets −1 and the row player gets 1. In other words the row player wins, which we may recognize as scissors winning against paper in the slightly less fantastical rock-paper-scissors.
In this game of Boulder-Parchment-Shears, I maximize my expected reward by playing each of the three strategies at probability (completely randomly). Similarly my opponent should do the same. If one of us were to adjust, playing Boulder more frequently, then the other can take advantage of this by increasing the rate at which they play Parchment to win more often. Playing each strategy at probability describes the unique Nash Equilibrium for the game of Boulder- Parchment-Shears. A Nash equilibrium a set of actions of each player such that each players action is the best response to all the other player’s actions. In the turn based Tic-Tac-Toe, we know that games always end in a tie when both players know the optimal (Nash Equilibrium) strategy.
But these are all descriptions of actual games and I promised you a story about trust. Soon I will describe the Trust Game, but before then I want to highlight the relevance of the Nash Equilibrium beyond the idea of an actual game. The strategies of a Nash Equilibrium are best responses to each other. If before an interaction (like a game), I announce that I will be playing the Nash-Equilibrium strategy, then assuming you believe me, you would be best served by also playing the Nash Equilibrium strategy.
Back to trust and wonderful humans
Alice is visiting Amsterdam for the first time in her life and after a visit to the Maritime Museum she stumbles upon the Marineterrein, a well-known hotspot for swimming in Amsterdam. She is lucky, it is one of the three scorching days and a swim would be fantastic right now. She makes for a group of strangers and asks them to watch her stuff while she takes a dip. Unfortunately for Alice this is where her luck ends, she was identified as a tourist and The Group of students take advantage of this: They remove the cash from her purse and disappear, never to be spotted by Alice again. The interaction between Alice and The Group can be modelled as the Trust game.
The Trust Game also involves two parties, though they only have two actions to choose from, and these are different per party. The truster (Alice) chooses whether or not to trust the Group (asking them to watch their items at the gracht). Subsequently, if Alice chose to trust, then the trustee (The Group) chooses whether to honour the trust (watch the items) or to abuse it (make a swift get-away with the cash on their swapfiets). This game is represented in matrix form by:
This game in particular may be even better represented in a game tree. This is because the moves 2 in this game are sequential; The Group only makes their decision (and indeed only has a decision to make) after Alice has placed trust. The game-tree of the trust game is shown in the figure below with as example the rewards possible when taking a swim on a warm summer’s day.
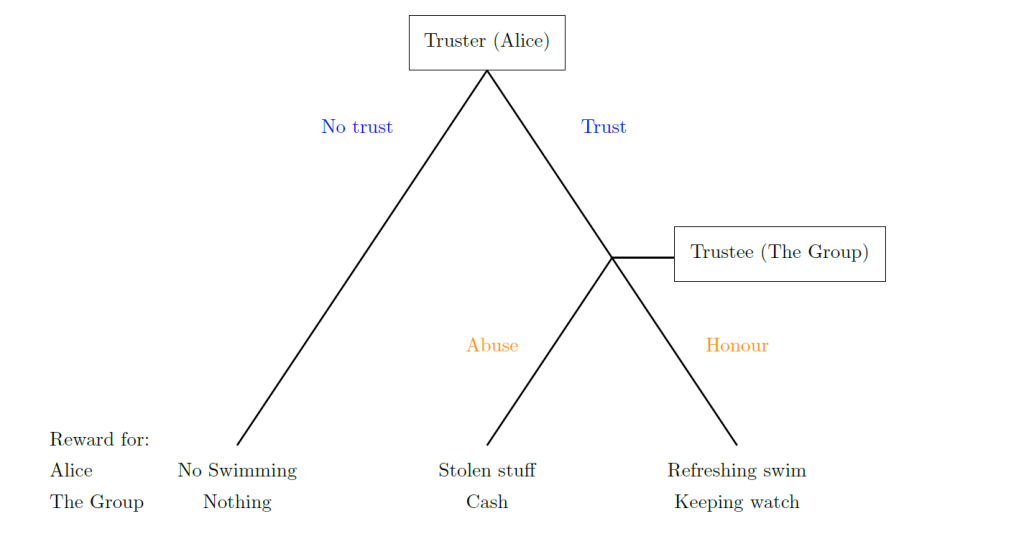
The trust game in game tree format.
Concluding thoughts and comments
Game Theory predicts that we would never swim on such a day or indeed; buy a used car, accept cookies when browsing, or vote for a politician to act in our favour. Though of course we have in some instances produced mechanisms to minimize the risk we take when performing the above actions, we clearly do still rely being able to trust others in our daily lives. This is of course no mistake, but simply shows us that some models do not capture everything required to make an accurate prediction. There could be various errors we make when modelling such a situation as a trust game, for instance, The Group of students (trustee) could get great joy out of letting tourists enjoy their favorite swimming spot, and so there is some benefit to keeping watch which was not captured in the original formulation. Whether it is the trust game which is modelled incorrectly or the assumptions that the players would act rationally I will not attempt to answer here. There are additions, modifications and developments in the field of game theory which try to answer the question how it can be that there is in fact quite a lot of trust in our societies.
Various possible solutions to this conundrum have been hypothesized which consider an evolutionary perspective (strategies as genes fighting for survival): Family relations between individuals make trust possible, direct (tit-for-tat) or indirect (reputation) reciprocity make trust possible, network structure make trust possible by getting to know the individuals close by and finally, because humans are somewhat ‘pack’ animals, a pack of cooperators outperforms a pack of defectors. (Nicky Case has created this wonderful game which illustrates the simple and powerful effect of repeated interactions) The research on these antecedents of trust and cooperation is not yet concluded. For now, I leave you with a thought: Models can be useful, but humans are wonderful, possibly irrational and definitely not so easily modelled.
Are you one of those people who always seems to pack just a bit too much for your car to handle when packing for a vacation? Then you should have a look at this article!
Imagine you’re in a remote village and only have a limited number of vaccines to distribute to protect the community from a deadly virus, who do you vaccinate?
A difficult decision, but necessary. Assuming that the disease is just as deadly for everyone in the community, the best way to prevent deaths is to contain the spread of the virus.
The part of the brain that controls the sleeping cycle is made up of two groups of neurons. In order for you to be able to sleep at night, the activity of these neurons needs to be synchronized with the cycle of the sun (e.g. active during the day and inactive at night). When you abruptly change the cycle of the sun (by flying to New York) these two groups need to re-synchronize to the new sun-cycle.
How can one hope to understand the precise structure of a virus if it is able to become unrecognizable within weeks? The mathematics behind this questions didn't let go of my mind for extensive periods of time during my PhD studies in Belgium.
(completely randomly). Similarly my opponent should do the same. If one of us were to adjust, playing Boulder more frequently, then the other can take advantage of this by increasing the rate at which they play Parchment to win more often. Playing each strategy at probability 
