Will you always reach your destination? This is the question to be answered.
Suppose that you are jumping from stone to stone on a lake. The stones are arranged as in the figure below.
We will call this formation of stones a orthogonal grid. When jumping from stone to stone you are only allowed to jump to the nearest neighbors. Hence when you are on one of the green stones below you are only allowed to jump on the yellow stones.
Hence you can't jump diagonally or on stones that are far away from the one you are standing on. Suppose that you start from the bottom left stone and you want to reach the top right stone. Then you can find many different paths to reach the end stone. But now it is that the game becomes interesting. We draw on every stone an arrow, like in the figure below.
On each turn, you move one square in the direction of the arrow, and then the stone you have departed turns 90° clockwise. If you’re not able to move because you are on a corner stone, then you remain on that stone and it turns 90° clockwise. The puzzle is to show that starting from the bottom left corner stone you will eventually reach the top right stone no matter how the arrows are when you start.
Exercise 1:
Consider first the orthogonal grid and show that no matter how the arrows are placed when you start you will always reach the end stone.
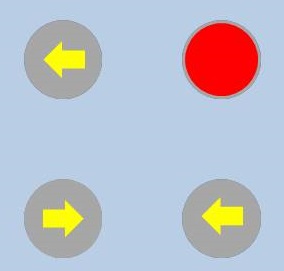Exercise 2:
Solve the same problem but for the 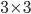orthogonal grid.
Exercise 3:
Can you also solve it for larger grids than the 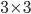one?
A conjecture of Erdős and Hajnal from 1989 says that forbidding any specific substructure results in existence of a very large homogeneous one! In this article you will have a look into one of the most fascinating problems in modern graph theory.
How can one hope to understand the precise structure of a virus if it is able to become unrecognizable within weeks? The mathematics behind this questions didn't let go of my mind for extensive periods of time during my PhD studies in Belgium.
In this article, dear reader, I am going to show you in which way the development of your opinion during the last political issue, the spread of a virus among your acquaintances during the current pandemic, and the alignment of some particles lying inside the device from which you are reading this article are extremely comparable phenomena.
If, after reading the title, your immediate response is to shout "1/6-th", then you have correctly answered the question. Well done! However, in this article we will focus on the meaning of this question. What exactly is this "chance" of which you've just exclaimed it equals 1/6-th?
Say you are living in Eindhoven and would like to spend a day in Amsterdam: what better way to get there than taking the train? Before your train departs, a whole logistic operation has taken place in the headquarters of the railway company to make this trip possible.
orthogonal grid. When jumping from stone to stone you are only allowed to jump to the nearest neighbors. Hence when you are on one of the green stones below you are only allowed to jump on the yellow stones.
orthogonal grid and show that no matter how the arrows are placed when you start you will always reach the end stone.
Exercise 2:
orthogonal grid.
