Can you always find a route through the bridges? This is the question to be answered.
The bridges of Kaliningrad (Königsberg)
Kaliningrad is a city located in the Russian exclave between Poland and Lithuania on the Baltic Sea. Suppose you are on vacation in this beautiful city and you are having a walk along the banks of river Pregol. As you walk towards the center of the city you see the small green island where the Cathedral of Königsberg is located. Probably many people have their walk on this small island, but how many actually know about the importance of this small island for modern mathematics?
Almost three hundred year ago, in 1736, the bridges surrounding this small island lead the great mathematician Euler to lay the foundations of graph theory, a field of mathematics that has grown immensely in the last decades!
Continuing your walk along the river you decide you want to make a small tour in this part of the city, you take the map of the city and you observe that there are five bridges connecting the different parts of the city with the island. What more natural to try and make a route passing from all bridges but only once from each one, this way you explore the whole area, you can walk on all the old bridges (three of the five) and also not spend too much time going back and forth.
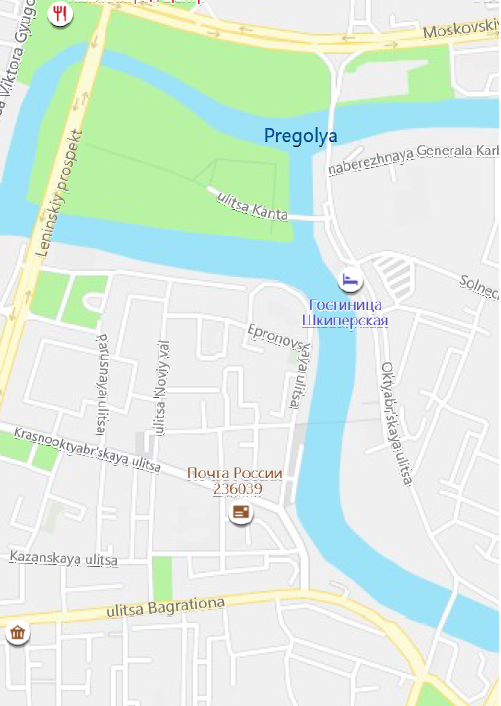
Figure 1: Map of Kaliningrad
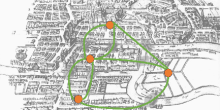
You immediately locate the five bridges on the map and you start trying to find a route passing from all the bridges but only once from each one. For easiness you depict the bridges, the island and the three parts of the city on a piece of paper using the following simple illustration
Figure 2: Illustration of the bridges
After some trials you find a route, follow the bridges as the colors indicate, Red - Blue - Yellow - Green - Purple!
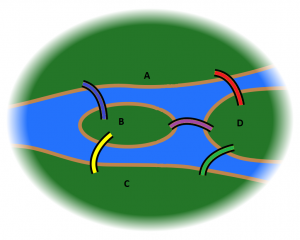
Figure 3: A possible route crossing all bridges once
As you were standing in area D, pure luck, this seemed like a good plan!
Exercise: Is it possible to find a route passing from all bridges once for all possible starting regions A,B,C and D?
After your walk, you have visited the Cathedral on the small island and you go and sit to a café to read a little bit more about the city. Browsing your guide you reach the chapter about the history of the city. Before World War II the city was named Königsberg and there were seven bridges instead of five, but two of the bridges were bombed during the war. Hence before World War II the route you have just found would not have worked due to the two additional bridges you should have taken into account!
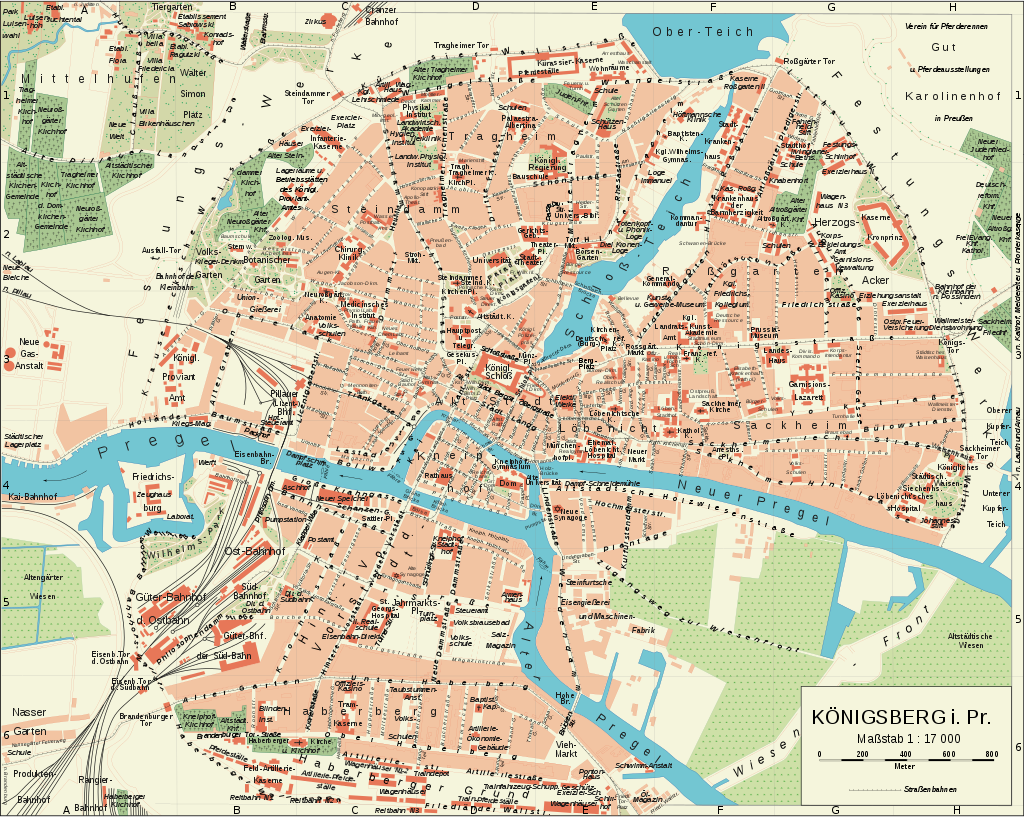
Figure 4: Map of Konigsberg from 1902
In this map from 1902 you observe that there were five bridges connecting the island with the main parts of the city, instead of three.
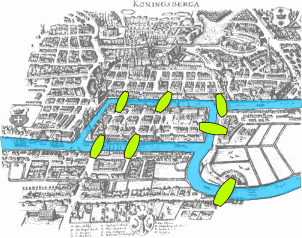
Hence the bridges, the island and the three districts can be illustrated as follows
Figure 5: Illustration of the bridges as they were in the past
You start wondering, would it be possible for a traveler in 1900 to cross from all the bridges just once? Euler was wondering exactly the same thing in 1736 when he solved this problem!
Exercise: Is it possible to find a route, starting from some arbitrary point on the map, and traversing all bridges only one time?
On a quiet afternoon, professor Meth is working in her office in Leiden on some tantalizing mathematics problems. Suddenly, someone knocking on her door nervously disrupts the silence.
In this article, we will discuss a mathematical riddle that "seems impossible even if you know the answer". It is better known as the 100 prisoners problem.
