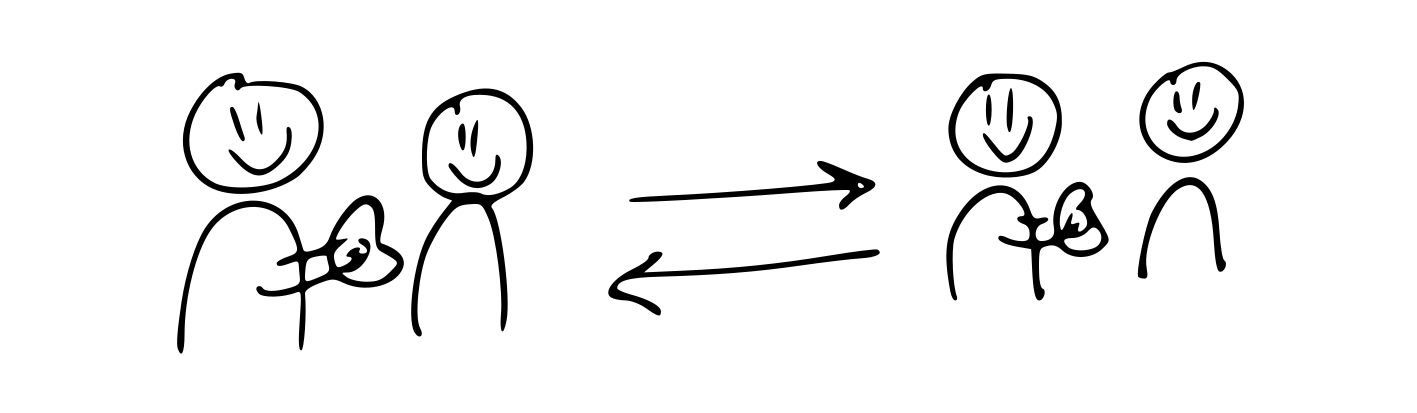
"Unfortunately, you are not a match", the doctor told them.
Still puzzled, and feeling tired from the dialysis treatments earlier this week, Ellis is slowly processing the news from the doctor. Just over two month ago, she heard from the doctor that her kidneys are failing to dispose waste products from her body. She has been diagnosed with end stage renal disease: the final stage of chronic kidney disease. At some point, the dialysis treatments will not be sufficient anymore, and a kidney transplant becomes necessary.
Her sister is willing to donate one of her kidneys, but the tests show that her blood type is not compatible for donating to Ellis. She cannot donate her kidney to Ellis.
Finding a matching donor can be a challenging task. Besides blood type, there are many medical factors that contribute to being a good match, such as tissue type. It may be the case that no relative or close friend is willing to donate and ticks all the required medical boxes.
However, when there are is another patient with a willing but incompatible donor, it may be the case that this donor is compatible with Ellis. When Ellis' sister is also compatible with the other patient, they can "swap" donors.
But how do you find such a cross-compatible pair? Specialized medical organizations have set up a so-called kidney exchange program that tries to match patient-donor pairs to each other. This happens both within a country such as The Netherlands, or even internationally between neighboring countries with similar medical programs. Doctors and hospitals provide a list of all patient-donor pairs that require a match. The list also contains relevant medical information about the patients and donors, to determine compatibility of the donated kidney. Finding compatible matches from this large list, is what mathematicians call the kidney exchange problem.
To find a solution to the kidney exchange problem, a mathematician's first step is to get rid of the unnecessary and mathematically unimportant details, such as the fact that the patients are named "Ellis" or "Bob", or the fact that they are human at all. Instead, every patient-donor pair gets reduced to a single "node" in a network. Two nodes are connected when both donors are compatible with the patients on the other side of the connection. What is left is a purely mathematical optimization problem: find as many matches in this network of compatible kidney exchanges. The question is however: is the number of matches the right thing to optimize?
Intuitively, maximizing the number of patients that are matched with a compatible donor makes sense. After all, it seems that helping the maximum number of patients increases the likelihood that a patient is matched. However, only maximizing the total number of matches does not tell you which patients are helped. It may be the case that multiple matchings help the same number of patients, but match different people. How would you feel if you are not part of the chosen matching in such an optimized system, while another matching that does include you also exists?
Below is an example, where there are multiple matching to choose from that all match four patients in total. The four patients are different in every matching, however.
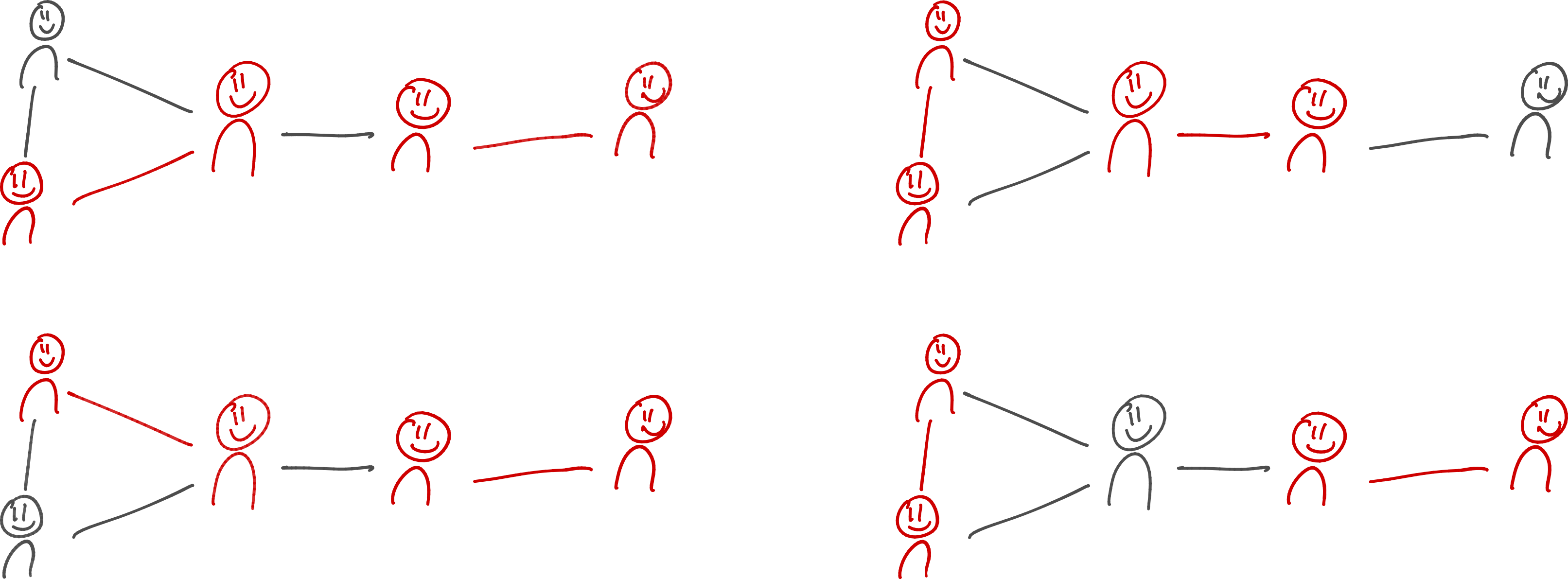
How do you avoid structurally disadvantaging certain patients? Sometimes there are medical reasons why certain patients more urgently need a match compared to others. But when every patient is considered to be equally important, it seems unfair to hard-to-match patients that they are left out.
When algorithms make decisions about people, these kind of fairness questions become relevant. Recently, unfairness in automated decision making has received attention with the Dutch childcare benefits scandal (de kinderopvangtoeslagenaffaire), issues with automated screening of job applications, and many other cases. In general, many of these cases confirm that fairness does not come "for free" when it is not explicitly accounted for.
To account for fairness in the kidney exchange problem, a solution is to choose not only one matching, but multiple. The decision maker first selects a diverse set of possible matchings. Then, one is chosen at random. In this manner, it can be viewed as a lottery of matchings, of sorts. As long as every patient is in at least one of the options in the lottery, all patients have at least some chance of receiving a kidney.
This is already more fair that just selecting one solution, but it can be the case that some patients have a lower chance in comparison with others. By optimizing the probability for every patient of receiving a kidney, we can try to make it more fair. In other words: maximizing the chance of every patient to "win" the lottery. The objective of the optimization problem has now shifted from just helping as many patients as possible, to helping every patient in a fair way.
Back to the example above, such an optimized lottery would consist of choosing one of the four matchings with each 25% probability. Since every individual patient is helped in at least three of the four possible options, each patient has 75% or higher chance that they are helped in this lottery.
Using the mathematical technique of linear programming, it is possible find a design for such a lottery that guarantees the maximum probability for every patient for receiving a kidney. It can even be used to ensure that every patient has the exact same chance!
In the example above, the probabilities of being helped are not the same for every patient. The second patient from the right is in every matching and thus has a probability of 100%. All other patients are in only three of the four possible matchings, corresponding to a probability of 75%. To make the probabilities the same of everyone, a different lottery as illustrated below is necessary.
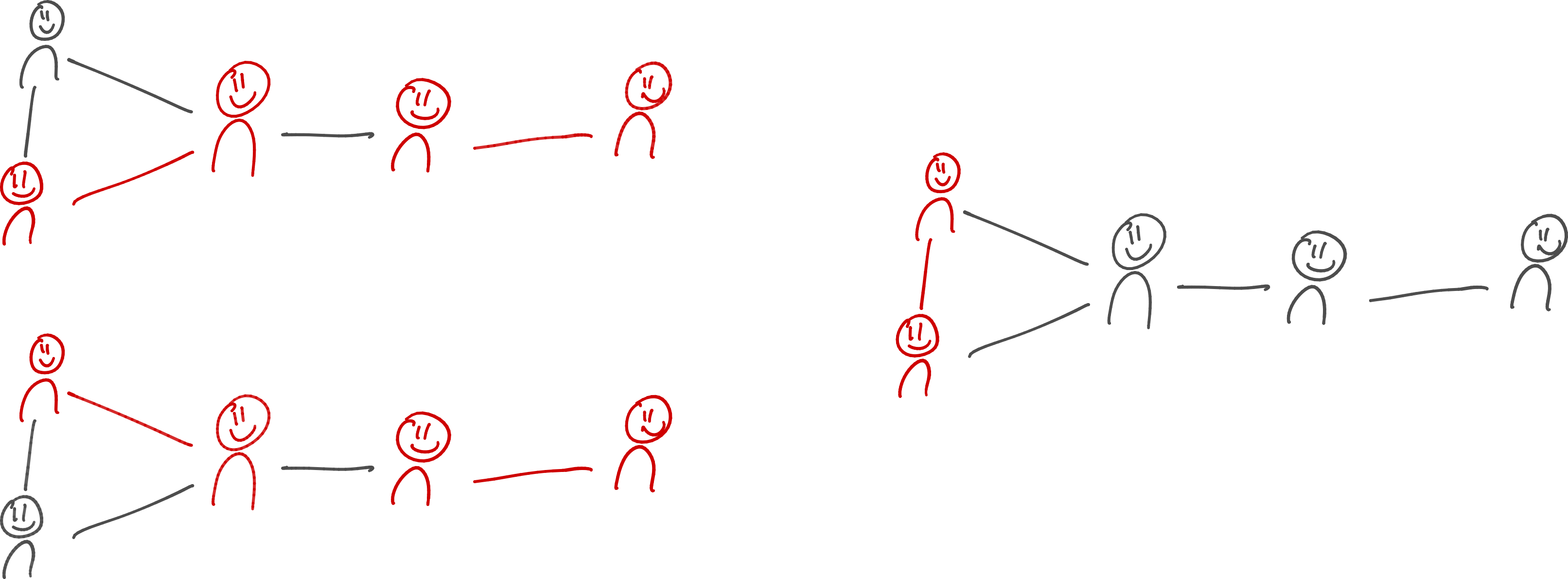
Choosing one of these three matchings with equal probability indeed makes sure that every patient is helped with the same chance, in this case 66%.
In fact, it can be shown that when the decision maker designs the lottery in such a way, the chance that every patient receives a kidney, is always guaranteed to be at least 66%. In other words, in the lottery, every patient has the exact same odds to win and these odds are 66% for every patient in the network. That is still remarkably high.
Equal odds of winning are fair, but in reality it may not be the most desirable option. For instance, if the matching on the right is chosen, there is another match that could have been made. In other words, one possible match is "wasted." In practice, this match should be made, to save as many lives as possible. Still, the lottery system as described here guarantees for every patient that they are matched with at least 66% probability. For some patients in the network, the chance of being matched may be higher. Sometimes, depending on what the network looks like, it is possible to do better than the 66% minimum. It is even possible to find a lottery of this kind with the highest possible minimum.
For Ellis, the kidney exchange program gives her the opportunity to still find a compatible kidney donor, even when her sister is not compatible with her. The fairness framework on top of the kidney exchange program gives not only her, but also all other patients the best chance possible to receive a kidney. Also for other decision-making problems that involve humans, it is worth to ask the question on how to incorporate "fairness by design". Who knows what this could do for algorithmic decision making in finance, governance, and many other areas, to optimize the chances for everyone.
It is quite difficult to extract information from your body. Your body is so vast that millions upon millions of messages get sent and deleted every second. It is impossible to know exactly who said something. The doctor’s main challenge is finding a way to reconstruct the network of interacting cells given the limited information she can measure.
How can one hope to understand the precise structure of a virus if it is able to become unrecognizable within weeks? The mathematics behind this questions didn't let go of my mind for extensive periods of time during my PhD studies in Belgium.
Imagine you’re in a remote village and only have a limited number of vaccines to distribute to protect the community from a deadly virus, who do you vaccinate?
A difficult decision, but necessary. Assuming that the disease is just as deadly for everyone in the community, the best way to prevent deaths is to contain the spread of the virus.
We want our guts to be filled with a diverse range of mutually beneficial and competitive interactions, a perfect blend of friends, frenemies, and enemies to keep our guts active and body on its toes. Read how networks can help understand these interactions!
