Networks can be found everywhere, and are also present in social media platforms such as Twitter. On Twitter, users can mention other users in their tweets, and can thereby interact with others. Generally, groups exist that send a lot of tweets to each other and far fewer tweets to users outside their group. Research has shown that words and phrases used in tweets are related to the group structure of users on Twitter. Hence, users in the same Twitter group generally also use similar words as their groupmates. If the research would be performed offline, it would for example mean that your classmates usually discuss school-related topics whereas your soccer team would talk about totally different topics such as how to win the next game. In this article, the research on word usages in Twitter social groups, also called communities, will be discussed in more detail.
In order to conduct the research, a dataset was constructed which consists of 189,000 different users and 75 million tweets between those users. A network was then constructed where all users are nodes, and a link between nodes was made when users sent mutually directed messages at each other. The next step was to identify the groups in this massive network. In order to identify the communities, an algorithm called maximum modularity was used. In short, this algorithm tries to find communities so that the proportion of messages between the users in each community is maximized. For example, in the offline setting, your classmates talk more to each other than to the members of your soccer team. This can be used to find the classmates community or the soccer team community.
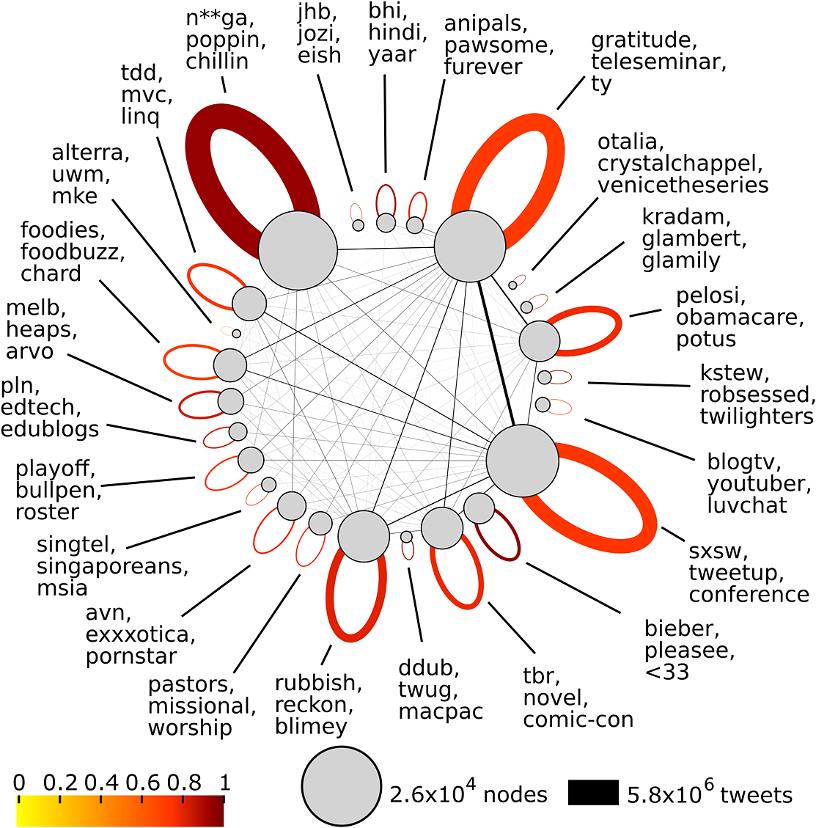
After the communities were detected, an algorithm was used to find characterizing words for each community. With your classmates, you will probably talk a lot about homework, teachers and assignments. On the contrary, with your teammates, you will use more often the words goal, strategy and winning. In the research, those words were found by looking at the difference in the fraction of users that used a word within the community with the fraction of users that used the word globally. It was then calculated whether the found difference could have happened by random chance. If it was very unlikely that the difference could have happened by random chance, it was a word that characterized the community. In the following figure, the characterizing words of the largest communities are shown:
Community structure on Twitter created by Word usages
Figure 1. Partition of users sampled from Twitter into communities. Adapted from: Bryden, J., Funk, S., & Jansen, V. A. (2013). Word usage mirrors community structure in the online social network Twitter, EPJ Data Science 2(3).
In Figure 1, circles represent different communities and the area of the circle indicates the size of the community. The width of the lines indicate the number of messages sent between different communities or within a community. The self-loop colors represent the proportion of messages that are sent within users from the same group.
Figure 1 shows that some communities clearly talk about a specific topic, such as the food community on the left (‘food’, ‘foodbuzz’) or the animal lovers community on top (‘anipals’, ‘pawsome’, ‘furever’). The authors have found that not only topics differed per community, but communities also differ in their language features. Some communities for example use more lengthened endings (‘pleasee’) than others. Another difference between communities is the usage of abbreviations in tweets.
To conclude, the authors have found that word usage mirrors the community structure of Twitter users. By identifying communities on Twitter, the authors are able to identify different cultural groups. With this information, it is also possible to predict the community a user belongs to, based on the words he is using in his tweets. Hence, if you use the word ‘pawsome’ a lot, a big chance exists that you are part of the animal lovers community.
Based on: Bryden, J., Funk, S., & Jansen, V. A. (2013). Word usage mirrors community structure in the online social network Twitter, EPJ Data Science 2(3)
An echo chamber is a community wherein the same opinions are bounced around, endlessly ‘echoing’ with barely any change. And as they do, any other opinion is shunned, pushed aside, and eventually just rejected without consideration.
Back in 2015, I joined the Movember health movement, a movement that you probably have heard of having something related to men growing a moustache. As a woman, you might imagine, I did not join for the moustache thing, but rather for the cause behind the moustache symbol, that is, raising awareness of prostate and testicular cancer.
We want our guts to be filled with a diverse range of mutually beneficial and competitive interactions, a perfect blend of friends, frenemies, and enemies to keep our guts active and body on its toes. Read how networks can help understand these interactions!
Since 2016 the world has been witnessing the Rohingya genocide in Myanmar, in 2021 we all saw the Capitol riots on tv. What do networks have to do with these events?
In the study of social networks, a key phenomena is the diffusion of information – how it travels from one individual to another across the network of people. An important question is how to identify the nodes with a high potential to spread information widely and deeper in the network.
