Road traffic analysis is one of the topics that receives a lot of focus in the NETWORKS program.
On 28 January 2022, Rik Timmerman (TU/e) defended his PhD Thesis titled 'Performance analysis at the crossroad of queueing theory and road traffic'. Are you courious to read what kind of questions about road traffic mathematicians try to answer? Below you can read a short description of Rik's research and also find some links to articles on the NetworkPages on this topic!
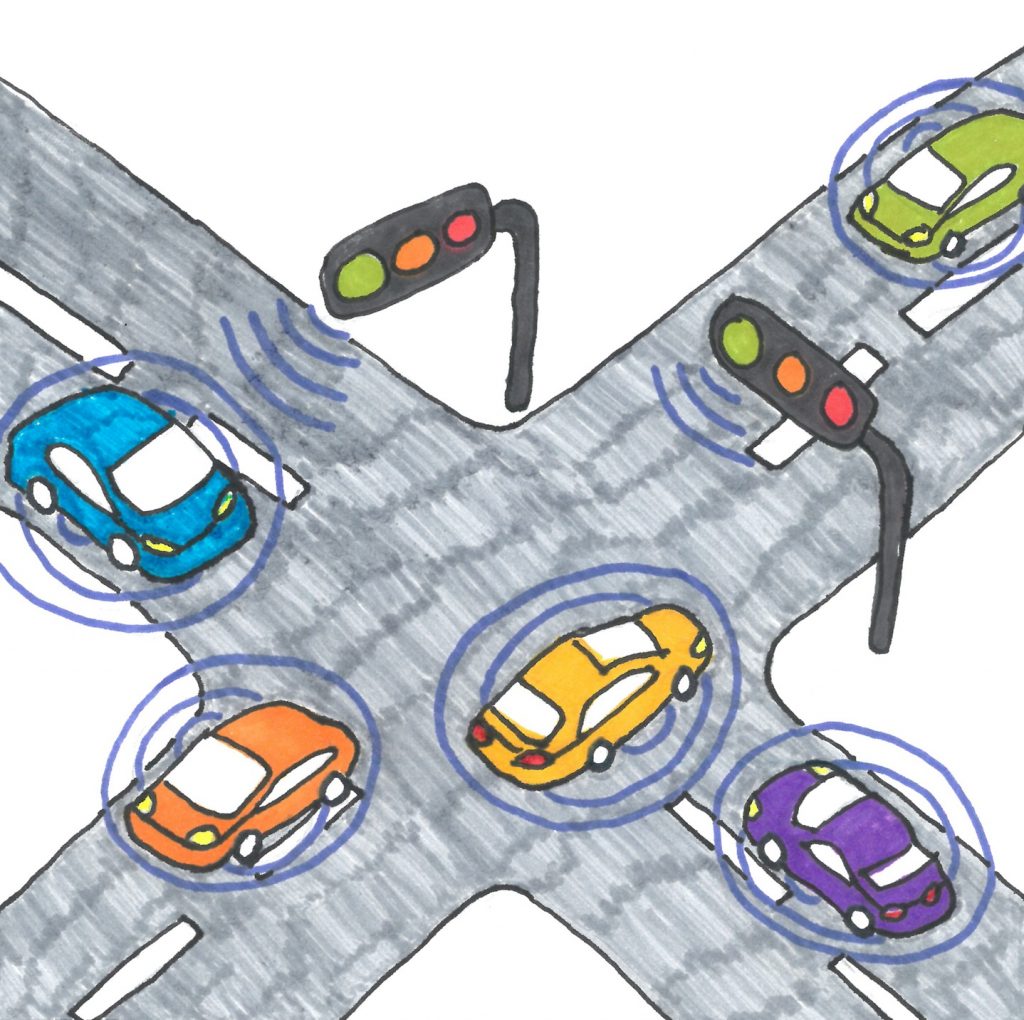
Image taken from Rik's article for the NetworkPages.
Performance analysis at the crossroad of queueing theory and road traffic
Congestion is a common phenomenon in road traffic. Despite all sorts of countermeasures, congestion remains an enormous societal problem. Mitigating the negative effects of congestion is a hard task and therefore a substantial body of research has been devoted to the prevention and reduction of congestion. Common sources of congestion are intersections, where many vehicles have to share a common scarce resource. Traffic-light control might be used to reduce some of the congestion if the control is well-adapted to the various traffic streams leading to the intersection. However, a good traffic-light control is typically difficult to obtain, e.g. due to randomness in the arrival times of vehicles at the intersection. Motivated by these observations, Rik and his collabotaros (among other things) deepen and extend the knowledge regarding traffic-light models that aim to represent such random influences.
In particular, they studied the so-called Fixed-Cycle Traffic-Light (FCTL) queue. Their analysis makes it possible to study a general rule to obtain the right balance between the green and red times which allows us to strike a balance such that, even when very busy, the queue in front a traffic light entirely dissolves often during the green period. This rule also makes it possible to find traffic-light settings that are close to the optimal settings.
They also studied several extensions of the FCTL queue such as scenarios where (turning) vehicles are blocked by pedestrians that receive a green light at the same time as the vehicles. Moreover, they investigated how the general rule to balance the green and red times performs when the green and red times are no longer fixed but depend on the number of vehicles waiting to cross the intersection. For such traffic-light models they also provide an approximate performance analysis, since the underlying queueing models are generally intractable.
Apart from the above, they also looked at a case with autonomous vehicles. In particular, they investigated how autonomous vehicles should approach an intersection and what the effect of platoon forming of arriving vehicles is on several performance measures. Subject to several criteria, they observed a large potential reduction in congestion. Finally, they studied congestion at highways. They developped a data-driven algorithm that enabled them to automatically identify so-called high-performance days, days with both a high traffic flow and no congestion. Ultimately, the easy identification of such days might lead to countermeasures against congestion on highways.
Rik carried his research out under the supervision of Prof. dr. J.S.H. van Leeuwaarden (Tilburg University and TU/e), Prof. dr. ir. I.J.B.F. Adan (TU/e) and Dr. ir. M.A.A. Boon (TU/e). This abstract is a slightly adapted version of the abstract on the website of NETWORKS. We would like to congratulate Rik and to wish him the best in his next step! The full thesis is also online available and can be found here. Would you like to read about a city without traffic lights? Then have a look at Rik's article for the NetworkPages.
On the Network Pages you can find more articles concerning methods used in the analysis of road traffic. There is something for all tastes, from general articles to more specific and in depth. In her article, Nikki Levering wrote about navigation systems, how they currently work and in which ways they could be improved to make better predictions. In his article, Jaap Storm dives a little bit deeper in the math and shows how a result from probability theory, the Central Limit Theorem, can be used to make predictions about traffic.
We can all agree, a no. 1 source of frustration is the endless waiting on hold for a call center agent to pick up the phone. Interestingly, over the last 111 years mathematicians have been working on a vast theory to solve this call center inefficiency.
In 2014, in the Netherlands, Belgium and Germany, the average person spend approximately 40 hours in a traffic jam - that is 5 work days! In this article, I will explain how mathematical models with uncertainty help traffic engineers to make decisions that improve traffic.
Traffic lights are currently an annoying but inevitable part of traffic. With the introduction of self-driving cars however, can we avoid having to wait for a red light ever again?
